Большая Энциклопедия Нефти и Газа
Сферическая линза
Параллельный пучок света [5] от сферической линзы , в главном фокусе которой помещен маленький освещенный диск, падал на манометр сзади. [16]
Операция двумерного фурье-преобразования, выполняемая простой сферической линзой над двумерным когерентным оптическим сигналом, является основной и элементарной в когерентной оптике. [17]
Иногда плоское окно приемника заменяют выпуклой сферической линзой , что позволяет получить дополнительное уменьшение изображения выходной щели. [19]
Рассмотрим еще один пример фокусировки сферической линзой частично когерентного светового пучка . [20]
В дополнение следует указать, что вместо сферических линз очень часто в осветительных системах, предназначенных для освещения щелей спектральных приборов, используют цилиндрические или сфероцилиндрические линзы. Они особенно пригодны при нитевидных источниках света. [21]
Получатся ли кольца Ньютона, если вместо сферической линзы использовать цилиндрическую. [22]
На рис. 17.16 и 17.17 представлены шесть типов сферических линз , а также условные изображения собирающих и рассеивающих линз. [23]
Геометрическое преобразование инверсии в пространстве связывает клин и сферическую линзу . В работах [43, 50, 56] показывается, что схожи и математические методы решения задач теории упругости для этих тел. В [50] метод сведения задачи теории упругости к обобщенной по И. Н. Векуа краевой задаче Гильберта распространяется на смешанную пространственную задачу для усеченного шара, сферическая поверхность которого жестко защемлена, а на срезе заданы нормальные напряжения, а также на аналогичную задачу для полупространства со сферической выемкой или выступом. Системы функциональных уравнений этих задач преобразуются к системам сингулярных интегральных уравнений. Излагаемая методика применима к исследованию задач для произвольной упругой сферической линзы, т.е. тела, образованного пересечением двух сфер разного радиуса. [24]
Оптический анализатор спектра ( рис. 5.19) использует способность сферической линзы осуществлять над приходящим электромагнитным сигналом преобразование Фурье. [26]
Но вследствие упругой деформации стекла невозможно добиться идеального соприкосновения сферической линзы и плоской пластинки в одной точке, поэтому более правильный результат получится, если вычислить R по разности радиусов двух колец гт и гп. [27]
Луч фокусируется на обрабатываемое изделие с помощью — набора цилиндрических и сферических линз . [28]
В таблице даны усилия затяжки для фланцевых соединений со сферическими линзами и прокладками восьмиугольного сечения. [29]
Источник
Описание экспериментальной установки. Наблюдение колец Ньютона и измерение их диаметров производится в данной
 |
Наблюдение колец Ньютона и измерение их диаметров производится в данной лабораторной работе с помощью измерительного микроскопа МИ–1. Плосковыпуклая линза и соприкасающаяся с ней стеклянная пластинка, закрепленные в специальной оправе, помещаются на горизонтальной плоскости предметного столика микроскопа. На объектив микроскопа надета насадка, в которой под углом 45˚ к оптической оси микроскопа закреплена тонкая стеклянная пластинка (рис. 3). Световой пучок, испускаемый лампой накаливания, частично отражается от нее и падает на пленку между линзой и стеклянной пластинкой. Отраженные от пленки лучи образуют интерференционную картину, которая рассматривается через окуляр микроскопа. (В условиях опыта микроскоп должен быть сфокусирован на выпуклую поверхность линзы в области ее касания со стеклянной пластинкой). В качестве источника света в работе используется осветитель ОИ-19, в выходном окне которого на соответствующей стадии эксперимента устанавливается светофильтр.
Механическая часть микроскопа позволяет плавно перемещать его тубус в направлении, перпендикулярном к оптической оси, и измерять перемещение с точностью 0,01 мм. Перемещение тубуса производится вращением специального барабана (со шкалой), связанного с держателем тубуса винтовой передачей.
В поле зрения окуляра микроскопа наблюдается визирная линия, которая в процессе измерений совмещается с выбранными точками в интерференционной картине.
Измерения и обработка результатов
Упражнение 1. Определение радиуса кривизны линзы.
Поместите на предметный столик микроскопа линзу со слегка прижатой к ней пластинкой так, чтобы точка их соприкосновения попала в поле зрения объектива. Сфокусируйте микроскоп на четкое изображение колец Ньютона. Установите в световой пучок светофильтр, пропускающий излучение известной длины волны (она указана на оправе светофильтра). Измерьте диаметры 1 и 4 темных интерференционных колец и по формуле (8) определите радиус кривизны поверхности линзы. Аналогичные измерения и вычисления проведите при m = 5, k =2, а также при m = 6, k =3. (Можно использовать и другие комбинации m и k). По результатам трех измерений вычислите среднее значение радиуса кривизны линзы; оцените погрешность ΔR его измерения данным методом.
Результаты измерений и вычислений сведите в табл. 1:
| № | 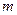 |  | 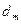 | 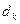 |  |  |  |
Упражнение 2. Определение длины световой волны.
Установите в световой пучок микроскопа другой светофильтр (по заданию преподавателя). Измерьте диаметры двух достаточно удаленных колец Ньютона и, используя формулу (8), вычислите длину волны света, пропускаемого исследуемым светофильтром, полагая радиус кривизны линзы известным из упражнения 1. Аналогичные измерения и вычисления проведите при двух других комбинациях номеров колец m и k. Вычислите среднее значение радиуса кривизны линзы; оцените погрешность Δλ его измерения данным методом.
Результаты измерений и вычислений сведите в табл. 2:
| № | 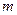 |  | 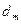 | 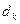 |  |  | 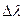 |
1. В чем заключается явление интерференции света? При каких условиях оно наблюдается?
2. Какие источники света называются когерентными?
3. Перечислите способы получения когерентных световых пучков. Как образуются когерентные пучки света при наблюдении колец Ньютона?
4. Сформулируйте условия возникновения максимумов и минимумов освещенности при интерференции световых пучков.
5. Чем отличаются интерференционные картины колец Ньютона, полученные в белом и монохроматическом свете?
6. Какой вид будет иметь интерференционная картина, если сферическую линзу заменить цилиндрической?
Интерферометр Линника
Цель работы: изучение оптической схемы и устройства интерферометра; определение длины световой волны; определение глубины царапины на полированной поверхности.
Приборы и принадлежности: микроинтерферометр МИИ–4, зеркало с внешним покрытием, исследуемый образец.
Литература: [1], § 171 – 175; [2], § 51; [3], § 16 – 20; [4], § 10 – 12; [5], § 139 – 140.
Интерференционные явления позволяют производить прецизионные измерения линейных и угловых размеров тел, показателей преломления веществ. Приборы, служащие для этих целей называются интерферометрами.
Классическим примером двухлучевого интерферометра является интерферометр Майкельсона. Интерферометр, изучаемый в данной работе, отличается от него лишь конструктивно. Принцип и схема микроинтерферометра МИИ–4 впервые были разработаны и применены для исследования качества обработки поверхностей академиком В.П. Линником.
*См. также введение к лабораторной работе № 4.
Оптическая система интерферометра и принцип
Оптическая схема интерферометра показана на рис. 1. Нить лампы накаливания 1 проектируется коллектором 2 в плоскость апертурной диафрагмы 3. В фокальной плоскости проекционного объектива 4 помещена полевая диафрагма 5, которая изображается объективом 4 в бесконечности.
После проекционного объектива параллельный пучок лучей попадает на разделительную пластинку 6, на одной стороне которой нанесено светоделительное покрытие. Разделительная пластинка делит падающий на нее пучок пополам: одну половину она отражает, другую – пропускает.
Пучок лучей, отраженных от пластинки 6, собирается в фокусе объектива 7 на исследуемой поверхности, и после отражения от нее снова проходит объектив 7, пластинку 6 и собирается в фокусе объектива 8, где возникает изображение исследуемой поверхности. Зеркало 9 направляет пучок лучей в визуальный тубус.
Второй пучок лучей, пройдя разделительную пластинку 6, падает на компенсатор 10, после чего собирается в фокусе объектива 11 на эталонном зеркале 12, отразившись от которого снова проходит через объектив 11, компенсатор 10 и падает на разделительную пластинку 6. При этом часть лучей проходит через разделительную пластинку 6 и не участвует в образовании изображения, а другая часть лучей отражается от пластинки 6 и интерферирует с лучами первой ветви интерферометра, образуя резкое изображение интерференционных полос в бесконечности. Это изображение объективом 8 и поворотным зеркалом 9 переносится в фокальную плоскость окуляра 13.
Таким образом, изображения интерференционных полос и исследуемой поверхности получаются в фокальной плоскости окуляра и налагаются друг на друга.
При вынутом окуляре наблюдаются два изображения апертурной диафрагмы 3, которые являются зрачками выхода системы; от их положения относительно друг друга зависят форма и положение полос, а также интервал между ними.
Для работы с монохроматическим светом, т.е. светом определенной длины волны, прибор снабжен двумя интерференционными светофильтрами 14, которые включаются и выключаются из хода лучей перемещением держателя светофильтров. Светофильтры отличаются друг от друга своими характеристиками. При фотографировании наблюдаемой картины зеркало 9 выключается из хода лучей и свет, пройдя через гомаль 15 и отразившись от зеркала 16, падает на поверхность матового стекла или фотопластинку 17.
Наблюдаемая интерференционная картина зависит от юстировки зеркала 12 и исследуемой поверхности, а также от характера пучка света, падающего на пластинку 6. Если падающий пучок параллелен, то при строгой перпендикулярности зеркала 12 и исследуемой поверхности все лучи в пределах поля зрения будут обладать одинаковой разностью хода. В зависимости от этой разности хода поле зрения окуляра 13 окажется темным или светлым. При перемещении исследуемого образца вверх или вниз будет происходить смена освещенности поля зрения.
При практическом применении прибора неподвижное зеркало 12 наклоняют на небольшой угол. В этом случае лучи, падающие на различные точки этого зеркала, проходят различные пути. Поэтому в окуляре будет наблюдаться уже не однородный фон, а система параллельных темных и светлых полос – полосы равной толщины, соответствующие равноудаленным от не отклоненного положения точкам зеркала. Смещение исследуемой поверхности вызовет перемещение этих полос. При смещении поверхности на величину, соответствующую половине длины волны (это соответствует изменению разности хода интерферирующих лучей на λ, т. к. луч проходит пространство между объективом 7 и исследуемой поверхностью дважды), полосы в поле зрения сместятся на один интервал. При смещении поверхности на Δl произойдет смещение интерференционной картины на N интервалов, причем N и Δ l связаны соотношением

Если на исследуемой поверхности имеются неровности, то в этих местах появляется дополнительная разность хода, что приводит к искривлению полос (рис.2).
Если измерить величину изгиба b интерференционной полосы и расстояние a между полосами, то можно найти глубину царапины d (или высоту неровности). Действительно, отношение b/a определяет, на сколько интервалов (N) произошел изгиб интерференционной полосы, и по (1)

С помощью прибора МИИ–4 можно достаточно точно измерить величину искривления, составляющую 0,1 интервала между полосами, что соответствует глубине царапины, равной 0,05 λ.
Внешний вид прибора показан на рис. 3. Исследуемый предмет помещается на предметный столик 1. С помощью двух микрометрических винтов столик можно перемещать в двух взаимно–перпендикулярных направлениях. Столик можно также поворачивать вокруг вертикальной оси. Осветитель 2 создает параллельный пучок света. Интерференционная картина наблюдается в окуляр 3, снабженный микрометром. Фокусировка оптической системы на исследуемую поверхность осуществляется с помощью головки 4, имеющей шкалу. Цена деления этой шкалы равна 0,003 мм.
Введение светофильтра осуществляется перемещением пластинки 5. В двух крайних отверстиях этой пластинки закреплены светофильтры разных характеристик (зеленый и желтый), среднее отверстие – свободное – используется при работе в белом свете. Вращением кольца (6) с накаткой изменяется отверстие апертурной диафрагмы (при уменьшении диаметра отверстия повышается контрастность интерференционной картины). Рукоятка 7 позволяет отключать (перекрывать) правое плечо интерферометра.
Измерения и обработка результатов
Включите лампу и положите на столик прибора зеркало с внешним покрытием поверхностью вниз. Рукоятку 7 (рис.3) поверните так, чтобы стрелка на ней была вертикальна. С помощью головки 4 сфокусируйте микроскоп на исследуемую поверхность. Поворотом рукоятки 7 включите правое плечо интерферометра (стрелка на рукоятке должна быть в горизонтальном направлении). При этом в поле зрения окуляра должны быть видны интерференционные полосы. Для получения большей контрастности полос нужно поворотом кольца 6 несколько уменьшить отверстие апертурной диафрагмы.
Упражнение 1. Измерение длины световой волны.
Перемещением пластинки 5 до упора введите в световой поток один из светофильтров. Наблюдая в окуляр интерференционную картину, плавно перемещайте оптическую систему интерферометра относительно поверхности зеркала с помощью головки микрометрического винта 4. Сосчитайте число интерференционных полос, прошедших в поле зрения при повороте головки на 3–4 деления. Зная цену деления головки микрометрического винта (0,003 мм), определите соответствующее изменение длины Δl вертикального плеча интерферометра. По формуле (1) найдите длину световой волны.
Упражнение 2. Определение глубины царапины.
Положите на столик прибора образец с полированной поверхностью. Сфокусируйте микроскоп на исследуемую поверхность. Вращением предметного столика добейтесь, чтобы царапина на поверхности была перпендикулярна интерференционным полосам. Окулярный микрометр 3 поверните так, чтобы одна из перекрещивающихся нитей была параллельна, а другая перпендикулярна полосам.
Определите расстояние в делениях окулярного микрометра между 10–15 темными интерференционными полосами. По этим данным найдите ширину а одной полосы.
Затем измерьте в делениях окулярного микрометра величину b изгиба интерференционных полос в области царапины (см. рис. 2). По формуле (2) найдите глубину царапины d.
1. В чем состоит явление интерференции света? При каких условиях оно наблюдается? Какие источники света называются когерентными?
2. Как обеспечивается когерентность световых пучков в интерферометре Линника?
3. Какой вид будет иметь интерференционная картина, полученная с помощью интерферометра Линника, если исследуемая поверхность и плоскость зеркала 12 (рис. 1) строго перпендикулярны, а пучок света а) параллельный; б) расходящийся?
4. Как будет изменяться интерференционная картина при параллельном пучке света, если изменять угол наклона зеркала 12?
5. Как изменится картина, если исследуемую поверхность сместить вдоль луча на расстояние, равное λ/4, λ/2, λ (λ – длина световой волны)?
6. Чем отличается искривление полос, соответствующее выступу и царапине на исследуемой поверхности?
Источник







