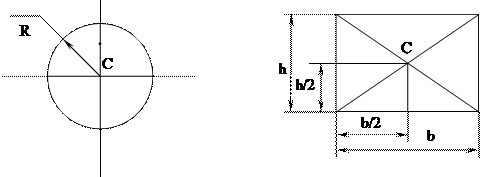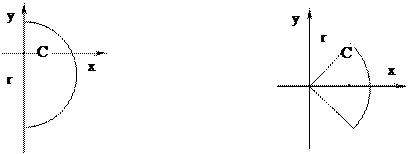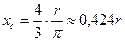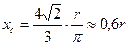Центр тяжести центры тяжести простейших геометрических сечений

Положения центров тяжести простых геометрических фигур

3) Центр тяжести любого треугольника лежит на пересечении медиан.

Частные случаи: для треугольника

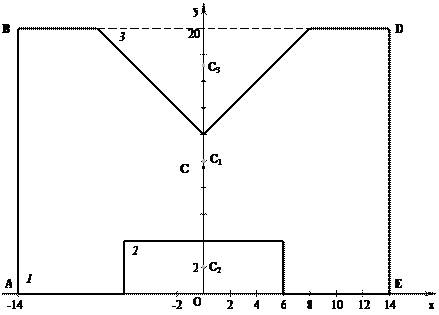
Пример 1: Определить положение центра тяжести фигуры, имеющей ось симметрии (размеры определены на схеме).

Фигура имеет ось симметрии, на которой находится центр тяжести. Совместим с осью симметрии ось y, а ось x – с нижним основанием фигуры.

Используем метод отрицательных площадей .

1. Разобьем фигуру произвольным образом на простые фигуры.

Наиболее рациональным из всех возможных способов деления фигуры на составные части является тот способ, при котором образуется наименьшее их число.

Дополнив фигуру до прямоугольника ABDE, разобьем ее на три части и определим площадь каждой (в см 2 ):

1 – прямоугольник (большой), 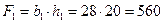(см 2 );

2 – прямоугольник (маленький), 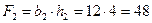(см 2 );

3 – треугольник, 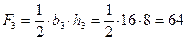(см 2 ).

2. Определяем координаты центров тяжести составных частей:

Точка С₁ – ЦТ первой фигуры имеет координаты: .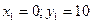

Точка С₂ – ЦТ второй фигуры имеет координаты: .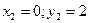

Точка С₃ – ЦТ третьей фигуры имеет координаты:

.

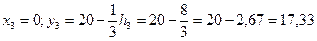
4. Координаты точки С — центра тяжести всей фигуры:

(см).

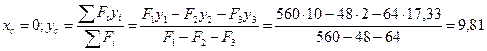
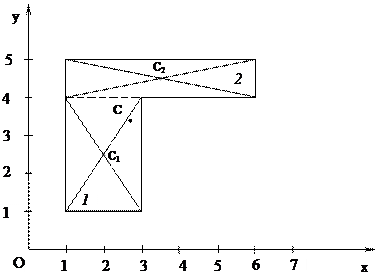
Пример 2: Определить положение центра тяжести фигуры, имеющей ось симметрии (размеры определены на схеме).

1. Разобьем фигуру произвольным образом на простые фигуры (в данном случае на два прямоугольника) определим площадь каждой (в см 2 ):

1 – прямоугольник, 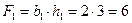(см 2 );

2 – прямоугольник, 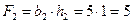(см 2 );

2. Определяем координаты центров тяжести составных частей:

Точка С₁ – ЦТ первой фигуры имеет координаты: .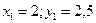

Точка С₂ – ЦТ второй фигуры имеет координаты: .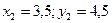

4. Координаты точки С — центра тяжести всей фигуры:

(см)

(см).

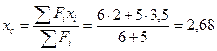
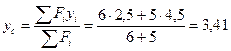
1. Яблонский А.А., Никифорова В.М. Курс теоретической механики. Ч.1. Статика. Кинематика. М.: Высш. шк., 2004.

2. Куприянов Д.Ф., Метальников Г.Ф. Техническая механика. М., 1995.

3. Цывильский В.Л. Теоретическая механика. М.: Высш. шк., 2004. – 343 с.

Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:

Источник

Определение геометрических характеристик

При расчёте элементов конструкций на прочность, жёсткость и устойчивость (классические расчёты в сопромате) используются следующие геометрические характеристики плоских сечений: площадь, моменты инерции, моменты сопротивления и другие.

Для простейших фигур, таких, как квадрат, прямоугольник, круг и т. д.– эти характеристики определяются по табличным формулам, для более сложных же поперечных сечений, как правило, состоящих из простых, характеристики нужно рассчитывать по специальным методикам.

Уроки по определению геометрических характеристик

В этом разделе ты сможешь найти уроки по расчёту различных геометрических характеристик, разного уровня сложности.

Нахождение центра тяжести сечения

В уроке рассмотрено сложное сечение, состоящее из простых фигур, для которого находятся координаты центра тяжести.

Нахождение осевых моментов инерции

В этом уроке рассмотрено симметричное сечение, состоящее из простых геометрических фигур, и для которого вычисляются осевые моменты инерции.

Справочные материалы для расчёта геометрических характеристик

В этом разделе ты найдёшь справочные материалы, которые могут понадобиться для расчёта геометрических характеристик.

Источник

Центр тяжести простых геометрических фигур

Центр тяжести составных плоских фигур.

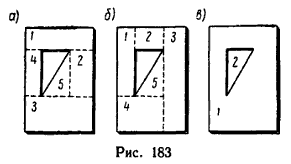
Иногда плоская пластина имеет такой вид, который позволяет разделить ее на составные части несколькими способами, например тонкую пластинку прямоугольной формы с треугольным вырезом (рис. 183). При определении положения центра тяжести такой пластинки ее площадь можно разделить на четыре прямоугольника (1, 2, 3 и 4) и один прямоугольный треугольник 5 – несколькими способами. Два варианта показаны на рис. 183, а и б.

Наиболее рациональным является тот способ деления фигуры на составные части, при котором образуется наименьшее их число. Если в фигуре есть вырезы, то их можно также включать в число составных частей фигуры, но площадь вырезанной части считать отрицательной. Поэтому такое деление получило название способа отрицательных площадей.

Пластинка на рис. 183, в делится при помощи этого способа всего на две части: прямоугольник 1 с площадью всей пластинки, как будто она целая, и треугольник 2 с площадью, которую считаем отрицательной.

Вес отдельной плоской фигуры можно представить так:
G_i = F_ip,
где F_i – площади каждой поверхности, а p – вес единицы площади фигуры, т.е. удельный вес.

После подстановки этого значения G_i в формулы

Центр тяжести простых геометрических фигур

.Центр тяжести – точка, через которую проходит линия действия равнодействующей элементарных сил тяжести. Он обладает свойством центра параллельных сил Поэтому формулы для определения положения центра тяжести различных тел имеют вид:
x_c = (∑ G_ix_i) / ∑ G_i;
(1) y_c = (∑ G_iy_i) / ∑ G_i;
z_c = (∑ G_iz_i) / ∑ G_i.

При решении некоторых задач на определение положения центра тяжести тел иногда необходимо знать, где расположен центр тяжести дуги окружности, кругового сектора или треугольника.

Если известен радиус дуги r и центральный угол 2α, стягиваемый дугой и выраженный в радианах, то положение центра тяжести C (рис. 176, а) относительно центра дуги O определится формулой:
(5) x_c = (r sin α)/α.

Если же задана хорда AB=b дуги, то в формуле (5) можно произвести замену
sin α = b/(2r)
и тогда
(5а) x_c = b/(2α).

В частном случае для полуокружности обе формулы примут вид (рис. 176, б):
(5б) x_c = OC = 2r/π = d/π.

Положение центра тяжести кругового сектора, если задан его радиус r (рис. 176, в), определяется при помощи формулы:
(6) x_c = (2r sin α)/(3α).

Если же задана хорда сектора, то:
(6а) x_c = b/(3α).

В частном случае для полукруга обе последние формулы примут вид (рис. 176, г)
(6б) x_c = OC = 4r/(3π) = 2d/(3π).

Центр тяжести площади любого треугольника расположен от любой стороны на расстоянии, равном одной трети соответствующей высоты. У прямоугольного треугольника центр тяжести находится на пересечении перпендикуляров, восставленных к катетам из точек, расположенных на расстоянии одной трети длины катетов, считая от вершины прямого угла (рис. 177).

10. Главные оси и главные центральные мом. инерции.

Оси, проходящие через центр тяжести сечения, называют центральными.Если фигура имеет ось симметрии, то последняя всегда проходит через центр тяжести фигуры, т. е. оси симметрии одновременно являются и центральными осями.Если элементарные площадки, выделенные в пределах рассматриваемого сечения, будем умножать на квадраты расстояний до оси, то получим осевые моменты инерции площадок. Суммируя моменты инерции всех площадок, найдем осевые моменты фигуры в целом:

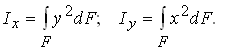Составляя интеграл, в котором подынтегральное выражение представляет собой произведение элемента площади на квадрат расстояния до начала координат (рис. 9.17), получим полярный момент инерции:

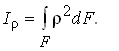Рис. 9.17. Схема к определению моментов инерции и моментов сопротивления.

Отметим еще одну характеристику, в которой площадка dF умножается на произведение координат

Эту величину называют центробежным моментом инерции. Приведенные моменты инерции измеряются в единицах длины» взятой в четвертой степени (, ).
Осевые и полярные моменты инерции фигуры — величины положительные и не могут быть равными нулю. Центробежный момент инерции в зависимости от положения осей может быть положительным или отрицательным, а также равным нулю. Две взаимно перпендикулярные оси, относительно которых центробежный момент инерции равен нулю, называют главными осями инерции и обозначаются . Для симметричной фигуры ось симметрии является и главной осью.
Осевые моменты инерции, определенные относительно главных осей, имеют максимальное и минимальное значения. Момент инерции сложной фигуры равен сумме моментов инерции образующих ее фигур. Подчеркнем, что сказанное справедливо в том случае, когда все моменты инерции вычисляются относительно одной и той же оси.
Для моментов инерции существует еще одно правило, часто используемое в расчетах. Применительно к осевым моментам оно «формулируется следующим образом: момент инерции фигуры относительно оси, параллельной центральной, равен моменту инерции относительно центральной оси плюс произведение площади фигуры, на квадрат расстояния между осями (рис. 9.18):

Рис. 9.18. Схема к определению моментов инерции относительно разных осей координат.

Для центробежных моментов инерции соответствующее правило в аналитическом виде выглядит так:

Источник