Практическое занятие №3.
Построение хода лучей в оптической системе

3.2. Задача построения изображения

Описание последовательности построения

Необходимы 2 луча, идущие через точку предмета. Пересечение преломленных лучей дает нам точку изображения.

1. Проводим луч через край предмета параллельно оптической оси. Преломленный луч пройдет через точку заднего фокуса.
2. Проведем луч через край предмета и точку переднего фокуса. Дальше луч пойдет параллельно оптической оси.
3. На пересечении построенных лучей находится искомое изображение точки предмета.

3.2.1. Положительная линза

1. Если предмет находится между линзой и ее фокусом, то его изображение – увеличенное, мнимое, прямое, и расположено оно по ту же сторону от линзы, что и предмет, и дальше от линзы, чем предмет.
   
2. Если предмет находится между фокусом и двойным фокусом линзы, то линза дает его увеличенное, перевернутое, действительное изображение: оно расположено по другую сторону от линзы по отношению к предмету, за двойным фокусным расстоянием.
   
3. Если предмет находится за двойным фокусным расстоянием линзы, то линза дает уменьшенное, перевернутое, действительное изображение предмета, лежащее по другую сторону линзы между ее фокусом и двойным фокусом.

3.2.2. Отрицательная линза

Отрицательная линза не дает действительных изображений, при всех положениях предмета дает уменьшенное, мнимое, прямое изображение, лежащее по ту же сторону от линзы, что и предмет.

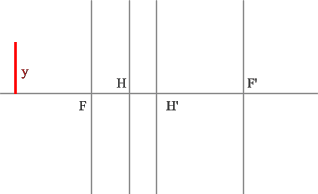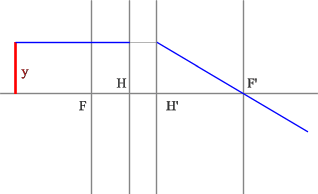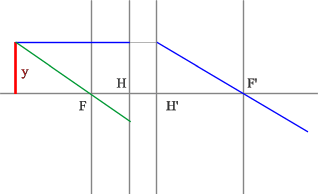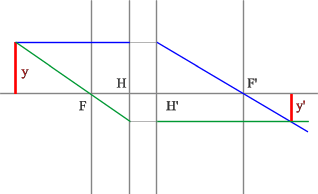
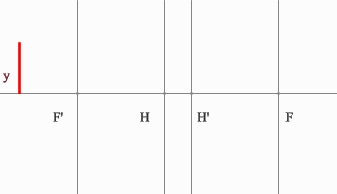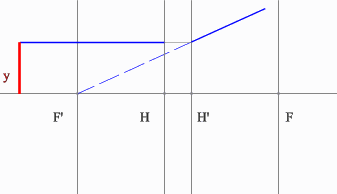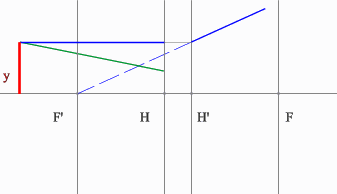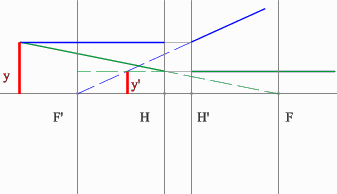
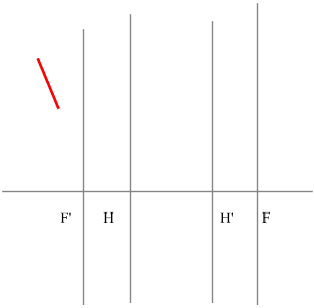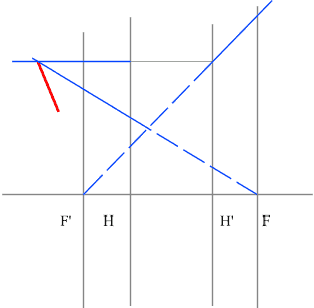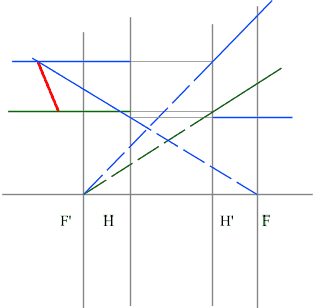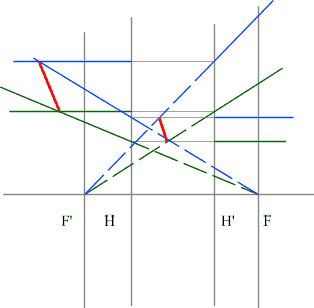
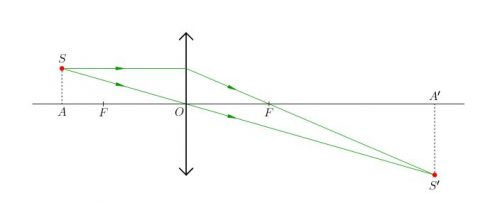
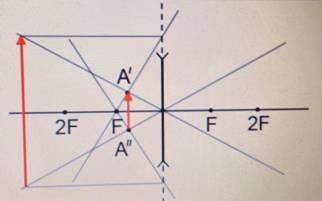
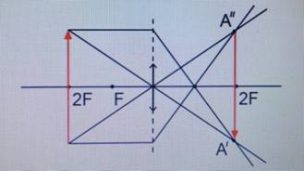
3.2.3. Построение изображения мнимого предмета

Построение изображения предмета, образованного пересечениями продолжений лучей в пространстве изображений решается так же, как и построение обычного предмета.

NB! Вспомогательные лучи лишь направляются к мнимому предмету, но, как и положено, до него не доходят, прреломляясь на главных плоскостях оптического элемента.

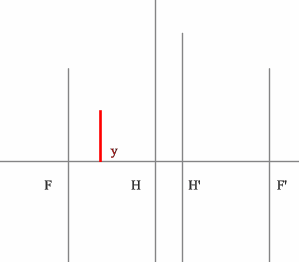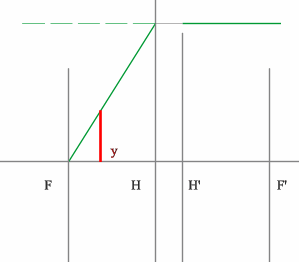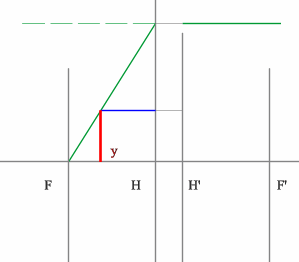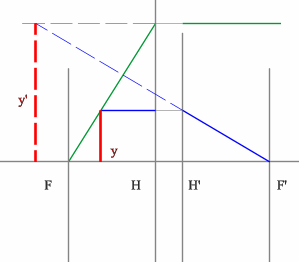
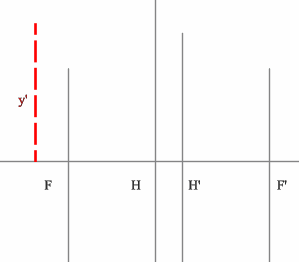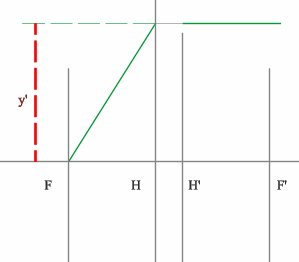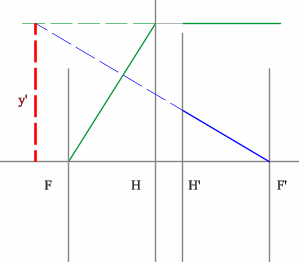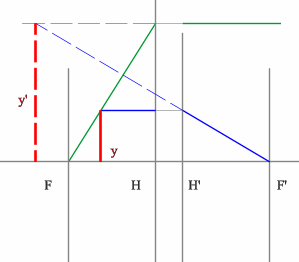
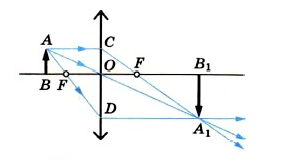
Рассмотрим пример: Красным обозначен предмет.

1. Зеленый луч проводим через край предмета и точку переднего фокуса. После оптического элемента луч пойдет параллельно оптической оси.
2. Синий луч направляется параллельно оси через точку предмета. По правилам преломления после оптического элемента, луч пройдет через задний фокус.
3. Изображение будет находиться на пересечении зеленого и синего лучей в пространстве изображений.

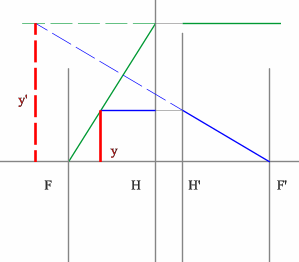
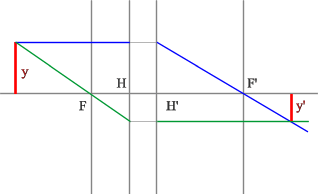
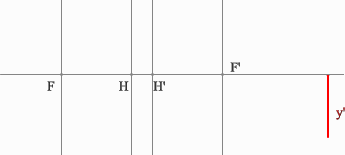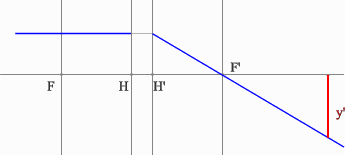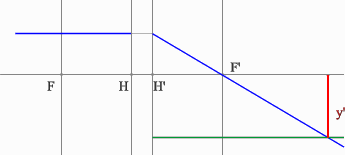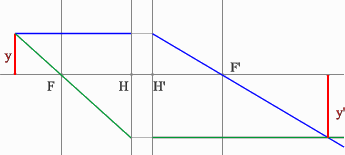
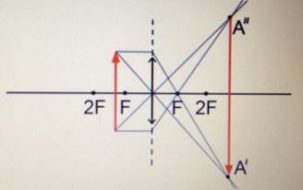
Рассмотрим пример: Красным обозначен предмет.

1. Зеленый вспомогательный луч так же проводим через передний фокус и край предмета. Не дойдя до мнимого предмета, луч преломится и пойдет параллельно оптической оси.
2. Синий луч направляется параллельно оптической оси через точку предмета. После оптического элемента луч пойдет через задний фокус.
3. Изображение у’ будет находиться на пересечении зеленого и синего лучей в пространстве изображений.

Источник

Практическое занятие №3.
Построение хода лучей в оптической системе

3.4. Примеры решения задач

3.4.1. Построение сложного изображения

Решение задач на построение сложного изображения сводится к более простой задаче и решается традиционным способом. Предмет, состоящий из нескольких точек строится как результат построения данных точек на предмете.

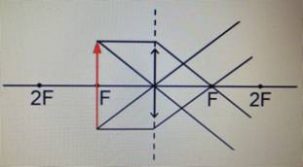
Задача 1.

Построить изображение предмета. Положительная линза.

Решение:

1. Сначала строим изображение нижней точки предмета розовыми лучами.
2. Затем — изображения второй точки синими лучами.
3. Соединяя эти точки, получаем изображение предмета.

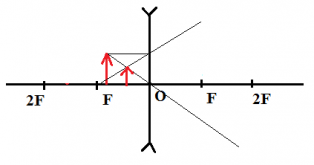
Задача 2.

Построить изображение предмета. Положительная линза.

Решение:

1. Сначала строим изображение верхней точки предмета синими лучами. Как и положено для рассеивающей линзы, пересекаться будут не сами лучи, а их продолжения.
2. Затем строим изображение второй точки зелеными лучами.
3. Соединяя эти точки, получаем изображение предмета.

3.4.2. Построение предмета по заданному изображению

Построение предмета по изображению сводится к решению обратной задачи. Суть та же, что и в построении изображения.

Необходимы 2 луча, идущие через точку изображения. Пересечение этих лучей в пространстве предметов, даст нам точку предмета.

1. Проводим луч через край изображения параллельно оптической оси. Преломленный луч пройдет через точку переднего фокуса.
2. Проведем луч через край изображения и точку заднего фокуса. В пространстве предметов луч пойдет параллельно оптической оси.
3. На пересечении построенных лучей находится искомое изображение точки предмета.

Положительная линза (построение предмета для действительного изображения)

Положительная линза (построение предмета для мнимого изображения)

Отрицательная линза

3.4.3. Определение положения кардинальных точек и плоскостей системы

Решение задач этого типа основано на том, что среда однородная. Поэтому правомерно проводить луч через центр линзы. Этот луч пойдет после системы под тем же углом, что и до системы. Угловое увеличение равно единице.

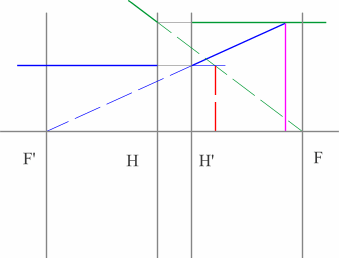
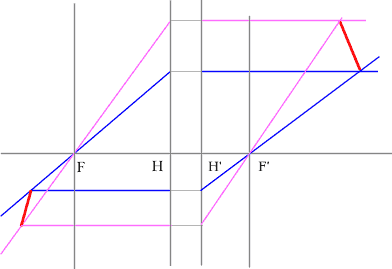
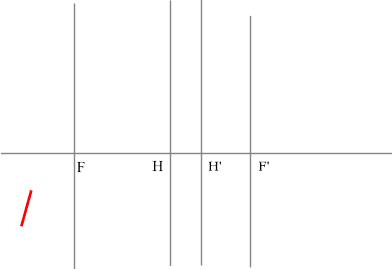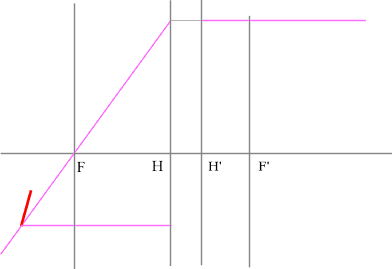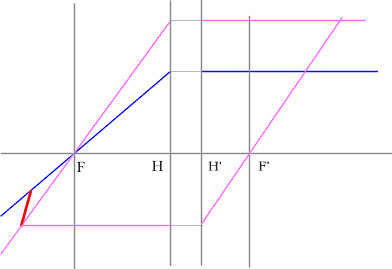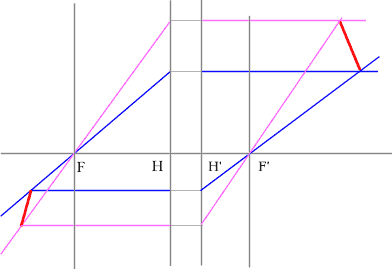
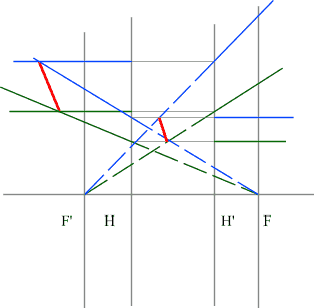
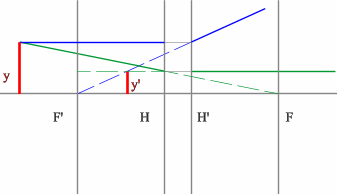
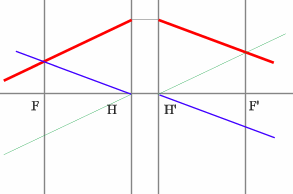
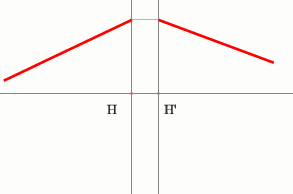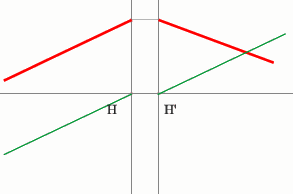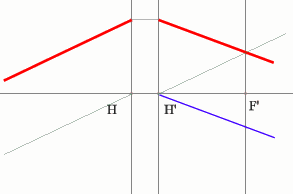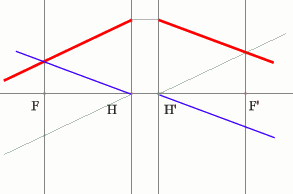
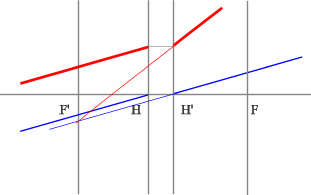
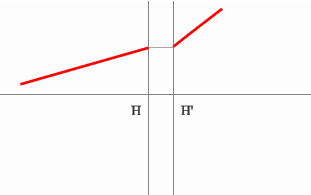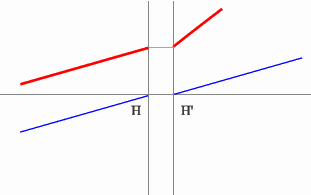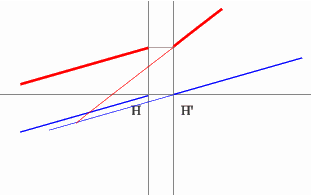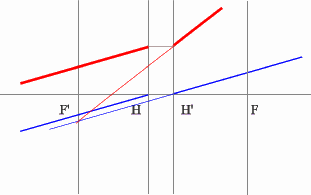
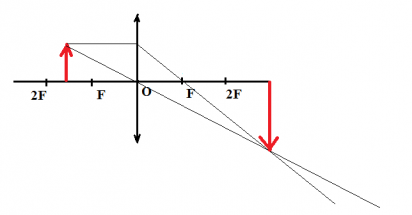
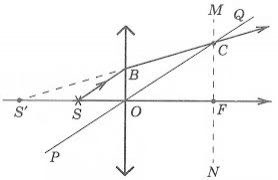
Задача 3.

Определить положение фокальных плоскостей по заданному ходу луча. Система находится в однородной среде.

Решение:

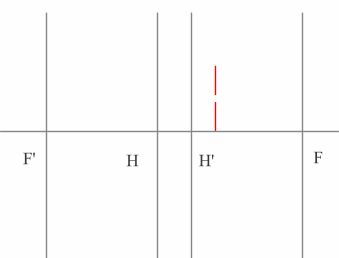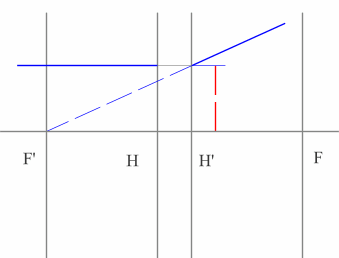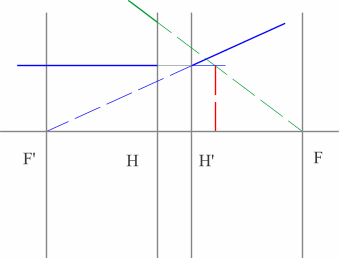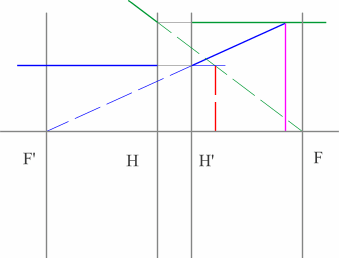
Для построения необходимо воспользоваться уже знакомым правилом: лучи, идущие параллельно друг другу, сойдутся в одной точке на задней фокальной плоскости.

Последовательность построения:

1. Строим луч параллельный заданному лучу через центр линзы. В пространстве изображений этот луч идет под тем же углом.
2. Находим точку пересечения заданного и построенного лучей в пространстве изображений.
3. По правилу, точка пересечения находится на задней фокальной плоскости системы.
4. Если среда однородная, то построение передней фокальной плоскости можно не производить, отложив полученное расстояние от передней главной плоскости.

Но на рисунке показано получение и передней и задней фокальных плоскостей с помощью построения:

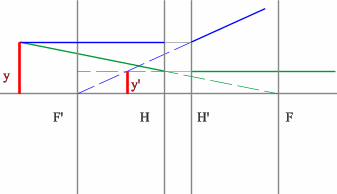
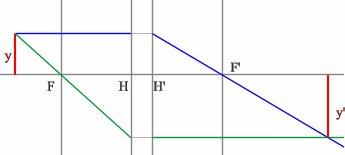
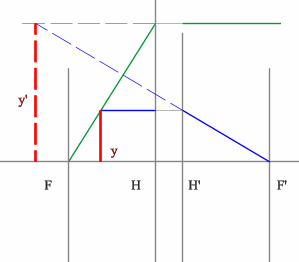
Задача 4.

Определить положение фокальных плоскостей по заданному ходу луча. Система находится в однородной среде.

Решение:

Строим синий луч, параллельный заданному в пространстве предметов.

Находим точку пересечения этого луча с заданным в пространстве изображений. Как видно из рисунка, пересекутся лишь продолжения лучей, что говорит о рассеивающем характере системы.

Через точку пересечения проходит задняя фокальная плоскость.

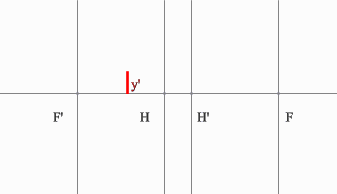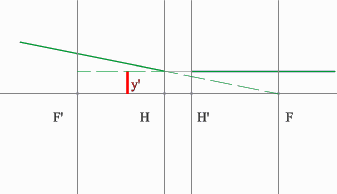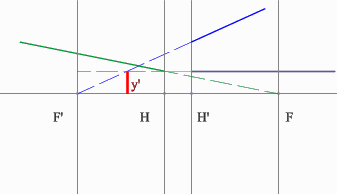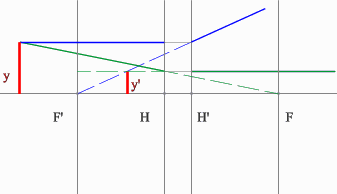
Поиск передней фокальной плоскости основан на том же принципе:

В пространстве изображений строим через центр линзы зеленый луч, параллельный заданному. В постранстве предметов этот луч пойдет под тем же углом и пересечет заданный луч в плоскости переднего фокуса системы. Найдя пересечение лучей, находим передний фокус.

Источник

Построение изображения в линзе | теория по физике 🧲 оптика

Свойства тонкой линзы определяются главным образом расположением ее главных фокусов. Поэтому, зная расстояние от источника света до линзы, а также ее фокусное расстояние (положение фокусов), мы можем определить расстояние до изображения, опустив описание хода лучей внутри самой линзы. Поэтому в изображении на чертеже точного вида сферических поверхностей линзы необходимость отсутствует.

Схематически тонкие линзы обозначают отрезком со стрелками на конце. Они смотрят от центра в противоположные стороны, если линза собирающая, и они направлены к центру отрезка, если линза рассеивающая.

Напомним, что линзы могут давать действительные и мнительные изображения. Причем, собирающая линза может давать как действительные, так и мнимые изображения. Рассеивающая линза всегда дает только мнимые изображения.

» href=»https://spadilo.ru/biologicheskij-vid-i-ego-kriterii/» data-gt-translate-attributes='[<"attribute":"data-cmtooltip", "format":"html">]’>вид самих изображений в линзе зависит от того, где расположен изображаемый предмет. Он может располагаться за двойным фокусным расстоянием, в фокальной плоскости второго фокуса, между вторым и первым фокусом, в фокальной плоскости главного фокуса и на расстоянии меньше фокусного расстояния линзы.

Вторым фокусом называют точку, которая расположена на главной оптической оси от главного фокуса на расстоянии, равном фокусному расстоянию линзы. Относительно линзы он располагается на расстоянии, равном двойному фокусному расстоянию линзы.

Построение изображения в собирающей линзе

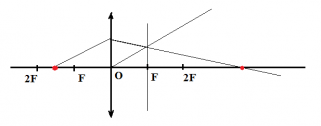
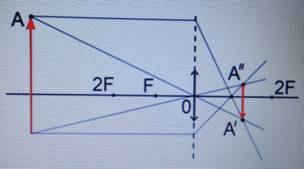
Предметы схематично изображаются в виде стрелки. Чтобы построить изображение предмета в собирающей линзе, нужно найти положение верхней и нижней точки этого изображения. Сначала находят положение точки изображения, соответствующей верхней точки предмета (точки А). Для этого из этой точки нужно пустить два луча:

Два вида лучей при построении изображений в линзе

Первый луч проходит из верхней точки предмета (точки А) параллельно главной оптической оси. На линзе (в точке С) луч преломляется и проходит через точку фокуса (точку F).

Второй луч необходимо направить из верхней точки предмета (точки А) через оптический центр линзы (точку О). Он пройдет, не преломившись.

На пересечении двух лучей обозначаем точку А₁. Это и будет изображение верхней точки предмета. Таким же образом нужно поступить с нижней точкой предмета. Но на пересечении вышедших из линзы лучей нужно поставить точку В₁. Изображение предмета при этом — А₁ В_1.

В зависимости от того, где расположен предмет, изображение может получиться действительным или мнимым, увеличенным или уменьшенным, перевернутым или прямым. Построим изображения для каждого из таких случаев.

Схема построения изображения	Расположение предмета относительно линзы + характеристика изображение
	Предмет располагается за двойным фокусом. Изображение: уменьшенное; перевернутое; действительное.
	Предмет располагается в фокальной плоскости второго фокуса. Изображение: перевернутое; действительное.
	Предмет располагается в пространстве между фокусом и двойным фокусом. Изображение: увеличенное; перевернутое; действительное.
	Предмет находится в фокальной плоскости. Изображения нет, поскольку лучи идут параллельно друг другу и не пересекаются.
	Предмет располагается между линзой и фокусом. Изображение: увеличенное; прямое; мнимое.

Пример №1. Построить изображение предмета, изображенного на рисунке. Определить тип изображения.

Чтобы построить изображение предмета, достаточно определить его положение одной точки — верхней. Поскольку предмет расположен параллельно линзе, для построения изображения, достаточно будет соединить найденную точку изображения для верхней точки предмета перпендикуляром, проведенным к главной оптической оси.

Чтобы построить изображение верхней точки, пустим от нее два луча — побочную оптическую ось через оптический центр и перпендикуляр к линзе. Затем найдем пересечение побочной оптической оси с преломленным лучом. Теперь пустим перпендикуляр к главной оптической оси и получим изображение. Оно является действительным, увеличенным и перевернутым.

Частный случай — построение изображения точки

Положение изображения точки можно найти тем же способом, описанным выше. Нужно лишь построить два луча и найти их пересечение после выхода из линзы (см. рисунок ниже). Так, изображению точки S соответствует точка S´.

Особую сложность составляет случай, когда точка расположена на главной оптической оси. Сложность заключается в том, что все лучи, которые можно построить, будут совпадать с главной оптической осью. Поэтому возникает необходимость в определении хода произвольного луча. Направим луч от точки S (луч SB) к собирающей линзе. Затем построим побочную оптическую ось PQ такую, которая будет параллельна лучу SB. После этого построим фокальную плоскость и найдем точку пересечения (точка С) фокальной плоскости с побочной оптической осью. Теперь соединим полученную точку С с точкой В. Это будет преломленный луч. Продолжим его до пересечения с главной оптической осью. Точка пересечения с ней и будет изображением точки S. В данном случае оно является мнимым.

Пример №2. Построить изображение точки, расположенной на главной оптической оси.

Чтобы построить изображение, пустим произвольный луч к линзе. Затем построим параллельную ему побочную оптическую ось и фокальную плоскость. Из места пересечения этой оси с фокальной плоскостью пустим луч, также проходящий через точку пересечения линзы с произвольным лучом. Построим продолжение луча до получения точки пересечения с главной оптической осью. Отметим точку пересечения — она является действительным изображением точки.

Построение изображения в рассеивающей линзе

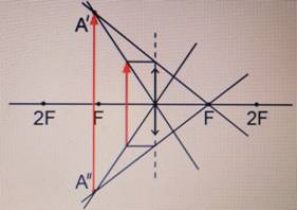
Чтобы построить изображение предмета в рассеивающей линзе, нужно определить положения точек изображения, соответствующих верхней и нижней точкам предмета. Вот как определить положение точки изображения для верхней точки предмета:

1. Нужно пустить луч, перпендикулярный главной оптической оси. Этот луч после преломления отклонится. Но его продолжение обязательно пересечет главный фокус линзы.
2. Нужно пустить луч от верхней точки предмета через оптический центр линзы (построить побочную оптическую ось).
3. Точку пересечения продолжения луча, полученного в шаге 1, с побочной оптической осью, нужно обозначить за изображение верхней точки предмета (на рисунке это точка А´).

Точно такие же действия нужно выполнить для нижней точки предмета. В результате получится точка пересечения, соответствующая изображению нижней точки предмета (на рисунке это точка А´´).

Внимание! Независимо от расположения предмета относительно рассеивающей линзы, изображение всегда получается прямым, уменьшенным, мнимым.

Пример №3. Построить изображение предмета в рассеивающей линзе.

Чтобы построить изображение, пустим от верхней точки предмета побочную оптическую ось через оптический центр и проведем перпендикуляр к линзе. Затем из точки главного фокуса проведем луч через точку пересечения линзы с перпендикуляром. Пересечение этого луча с побочной оптической осью есть изображение верхней точки предмета. Теперь проведем от нее перпендикуляр к главной оптической оси. Это и будет являться изображением предмета. Оно является мнимым, уменьшенным и прямым.

Построение изображений в плоском зеркале

Плоское зеркало — это плоская поверхность, зеркально отражающая свет.

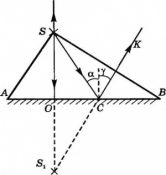
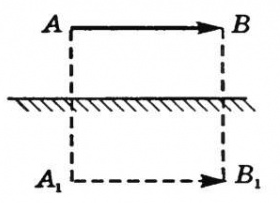
Построение изображения в зеркалах основывается на законах прямолинейного распространения и отражения света. Продемонстрируем это с помощью рисунка ниже.

Построим изображение точечного источника S. От точечного источника света лучи распространяются во все стороны. На зеркало падает пучок света ASB, и изображение создается всем пучком сразу. Но для построения изображения достаточно взять любые два луча из этого пучка. Пусть это будут лучи SO и SC. Луч SO падает перпендикулярно поверхности зеркала АВ. Поскольку угол между ним и перпендикуляром, восстановленным в точке падения, равен 0, то угол падения принимаем равным за 0. поэтому отраженный пойдет в обратном направлении OS. Луч SC отразится под углом γ=α. Отраженные лучи OS и СК расходятся и не пересекаются, но если они попадают в глаз человека, то человек увидит изображение S₁, которое представляет собой точку пересечения продолжения отраженных лучей.

Таким образом, чтобы получить изображение в плоском зеркале, нужно:

• Пустить от источника света луч, перпендикулярный к плоскости зеркала (падающий луч совпадает с отраженным лучом).
• Пустить от источника света к плоскости зеркала еще один луч под произвольным углом.
• Построить отраженный луч от падающего луча, построенного в шаге 2, используя закон отражения света.
• Найти пересечение продолжений отраженных от зеркала лучей (пущенного под прямым углом и произвольным углом).

Внимание!

Изображение в зеркале всегда является мнимым. Это связано с тем, что изображение строится на пересечении продолжении лучей, а не на самих лучах.

Изображение в плоском зеркале находится от зеркала на таком же расстоянии, как предмет от этого зеркала. Это легко доказать тем, что треугольники SOC и S₁OC равны по стороне и двум углам. Следовательно SO = S₁O. Отсюда делаем вывод, что для построения изображения точечного источника света достаточно знать расстояние, на котором он находится от зеркала. Останется только провести к зеркалу перпендикулярную прямую и отложить на ней точку на нужном расстоянии.

При построении изображения какого-либо предмета последний представляют как совокупность точечных источников света. Поэтому достаточно найти изображение крайних точек предмета. Так, изображение А₁В₁ соответствует предмету АВ.

Изображение и сам предмет всегда симметричны относительно зеркала.

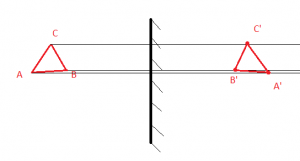
Пример №4. Построить изображение треугольника ABC в плоском зеркале.

Чтобы построить изображение, пустим к плоскому зеркалу перпендикулярные прямые. Затем измерим расстояние от каждой точки до зеркала и отложим их по перпендикуляру от зеркала в обратную сторону. Так для точки А мы находим точку А´, для В — В´, для С — С´.

Видно, что треугольник отразился зеркально (изображение и предмет симметричны друг другу). Так и должно быть в случае с зеркалом.

Равнобедренный прямоугольный треугольник ABC расположен перед тонкой собирающей линзой оптической силой 2,5 дптр так, что его катет AC лежит на главной оптической оси линзы (см. рисунок). Вершина прямого угла C лежит ближе к центру линзы, чем вершина острого угла A. Расстояние от центра линзы до точки A равно удвоенному фокусному расстоянию линзы, AC = 4 см. Постройте изображение треугольника и найдите площадь получившейся фигуры.

Источник