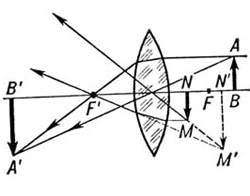
- Почему при рассмотрении предмета через лупу он переворачивается?
- Почему изображение через линзу перевернутое
- Изображение предмета, даваемое линзой
- Изображение предмета и фокус линзы
- Построение изображения предмета, находящегося за двойным фокусом линзы
- Характеристики изображения предмета
- Изображение предмета, находящегося между фокусом и двойным фокусом собирающей линзы
- Изображение предмета, находящегося перед фокусом собирающей линзы
- Выводы
- Памятка построения изображений предмета
- Пример построения изображения
Почему при рассмотрении предмета через лупу он переворачивается?
При рассмотрении предмета, через лупу, на дальнем расстоянии, он переворачивается в обзоре лупы.
Существует такие понятия, как фокус линзы, а так же прямое и обратное изображения.
Фокус линзы: точка, в которой сходятся (пересекаются) преломленные линзой лучи.
Прямое изображение — ориентация наблюдаемого через линзу объекта сохраняется. Низ снизу, верх сверху.
Обратное изображение — ориентация не сохраняется. Низ перемещается вверх, верх — вниз.
Так вот существуют лупы, двояковыпуклая линза которых до фокуса дает действительное прямое изображение, а после — действительное обратное.
d — «расстояние наилучшего зрения», считается 25 см
F — фокусное расстояние линзы, определяется фокусированием лучей Солнца в минимальное пятно.
На фокусное же расстояние влияют радиусы кривизны сторон линзы и коэффициент преломления материала линзы.
Из жизненного опыта могу сказать, что специальными очками-лупами пользуются часовщики, ювелиры, а также косметологи.
А вот как распределились популярные ответы людей на этот вопрос в игре:
• сыщик / детектив / следователь
Все что по форме похоже на линзу и может преломлять солнечный свет и концентрировать его пучки: 2 стеклышка от механических часов, скрепленные друг с другом, пространство между которыми заполнено водой (привет Жюль Верн), донышко от алюминиевой банки, ложка (возможно придется её погнуть для придания нужной формы, половник, наполненные водой электрическая лампочка и презерватив, тоже представляют собой хорошую линзу, если повозиться, можно сделать линзу даже из куска чистого льда и при помощи неё развести огонь.
Вдавив тела в диваны тесные
Но, вперив в карты очи чесные,
Коль через лупу посмотреть
Истерзаных своих мечтаний
Через игру нам не обресть!
Небрежность наших отношений
Нам стоит многих прегрешений!
Непосредственно при измерении твердости металлов лупа не применяется. Как верно подметил vadzimvip, принцип измерения твердости основан на вдавливании (с определенной силой) в поверхность металла некоторого элемента, и дальнейшего измерения размера отпечатка, оставленного этим элементом. Конус алмазный с углом при вершине 120 градусов применяется в методе Роквелла. Алмазная пирамидка – в методе Виккерса. Стальные закаленные шарики в методе Бринелля (диаметр шарика -2,5; 5 и 10 мм) и в методе Роквелла (диаметр шарика 1,588 мм). Обратив внимание на диаметр шарика в методе Роквелла, становится понятно, что размеры отпечатков должны быть измерены с высокой точностью. Иногда до тысячных долей миллиметра. Лупа такую точность дать не может. Поэтому для измерения отпечатков применяют измерительные микроскопы. Но и лупа, тоже нужна при работах по измерению твердости металлов. Лупа с увеличением 5 крат применяется для внешнего осмотра наконечников (шариков, пирамидок, конусов) на предмет выявления на них имеющихся дефектов.
Источник
Почему изображение через линзу перевернутое
1. Какое свойство линз позволяет широко использовать их в оптических приборах?
Получение изображения предмета.
2. В зависимости от чего меняются изображения, даваемые собирающей линзой?
В зависимости от того, на каком расстоянии находится предмет от линзы.
Изображения, даваемые собирающей линзой, зависят от места расположения предмета относительно линзы.
3. Как строилось изображение предмета, находящегося между фокусом и линзой, и каковы свойства этого изображения?
Изображение предмета между фокусом и линзой:
— построить ход двух лучей, исходящих из точки: первый луч — параллельно оптической оси, второй луч — через оптический центр линзы;
— за линзой эти лучи будут расходящимися и не пересекутся;
— изображение точки в этом случае даст пересечение продолжений этих лучей с той же стороны линзы, где находится сам предмет;
— т.к. предмет перпендикулярен оптической оси и один его конец находится на ней, то изображение предмета также будет перпендикулярно к оптической оси;
— из полученной точки изображения провести отрезок перпендикулярно оптической оси до пересечения с ней — это изображение предмета;
— полученное изображение является мнимым, прямым, увеличенным, находится по ту же сторону от линзы , что и сам предмет.
4. При каких условиях линза даёт уменьшенное, действительное изображение предмета? Где оно расположено?
Предмет находится за двойным фокусным расстоянием линзы.
В этом случае линза дает уменьшенное, перевернутое, действительное изображение предмета, лежащее по другую сторону линзы между ее фокусом и двойным фокусом.
5. При каких условиях линза даёт увеличенное, действительное изображение предмета? Где оно расположено?
Если предмет находится между фокусом и двойным фокусом линзы, то линза дает его увеличенное, перевернутое, действительное изображение.
Оно расположено по другую сторону от линзы по отношению к предмету, за двойным фокусным расстоянием.
6. Почему изображения предметов, находящихся на расстоянии большим, чем 2F от собирающей линзы, являются действительными?
Лучи, исходящие от точки, находящейся на расстоянии от линзы, большем, чем двойное фокусное, проходят через линзу и пересекаются за ней.
Изображение точки, получаемое на пересечении самих лучей, называется действительным.
6. В каких оптических приборах используются линзы?
Линзы применяются в в фотоаппаратах, микроскопах, биноклях, очках, телескопах и т.д.
7. Почему вогнутая линза не даёт действительного изображения?
Рассеивающая линза не дает действительных изображений, так как лучи, прошедшие сквозь нее, расходятся.
Изображение точки получается на пересечении не самих лучей, а их продолжений.
8. Как строится изображение в рассеивающей линзе. Каким оно бывает?

Рассеивающая линза при всех положениях предмета дает уменьшенное, мнимое, прямое изображение, лежащее по ту же сторону от линзы, что и предмет.
Источник
Изображение предмета, даваемое линзой
Используя лупу, мы видим увеличенное изображение предмета. Другие линзы уменьшают действительные размеры предмета. От чего же это зависит? Как правильно построить изображение, даваемое линзой?
На прошлом уроке мы с вами научились строить изображения светящейся точки, даваемое собирающей или рассеивающей линзой. Теперь перед нами стоит задача выяснить закономерности получения различных изображений предмета и научиться самостоятельно их получать с помощью чертежей.
Изображение предмета и фокус линзы
Рассмотрим простой опыт, схожий с тем, что был в прошлом уроке. У нас так же имеется большая собирающая линза, но вместо маленькой лампочки — свеча (рисунок 1). Свечу мы уже можем рассматривать как протяженный предмет. Поместим ее между линзой и ее фокусом $F$.
Теперь посмотрим на свечу через линзу. Мы увидим ее изображение с той же стороны, где она действительно находится.
Но нам будет казаться, что свеча находится немного дальше своего истинного положения. Кроме того, изображение будет увеличенным.
Изображение не будет наклоненным или перевернутым. Такое изображение называется прямым.
Если мы начнем перемещать свечу относительно ее фокуса (ближе и дальше от линзы), то увидим, что ее изображение будет существенно изменяться. Например, если мы переместим свечу за фокус линзы, то изображение пропадет. Но при этом оно появится с другой стороны линзы, далеко от нее. Чтобы его увидеть, нужно расположить экран с той стороны, где на рисунке 1 находится Образавр.
Это изображение будет не только увеличенным, но и перевернутым по отношению к свече.
Значит, передвигая свечу на различные расстояния от линзы и ее фокуса, мы можем получить различные изображения.
Построение изображения предмета, находящегося за двойным фокусом линзы
Теперь мы можем рассмотреть, как строятся изображения протяженных предметов, находящихся на разных расстояниях от собирающей линзы.
Разберем рисунок 2. Мы провели оптическую ось и отметили на рисунке собирающую линзу. По обе стороны от нее отметили две равноудаленные точки — фокусы линзы $F$. Так же мы отметили двойные фокусные расстояния — $2F$.
Предмет на чертежах мы будем изображать с помощью стрелки. Ее концы отмечаем точками $A$ и $B$. Такое обозначение поможет нам легко оценивать полученное изображение: будет оно прямым или перевернутым.
Начнем с того, что поместим наш предмет за двойной фокус линзы.
Чтобы получить изображение предмета, даваемое линзой, нам необходимо получить изображения двух точек $A$ и $B$ и соединить их между собой.
Получим изображение точки $A$. Для этого начертим ход двух световых лучей, выходящих из этой точки:
- Луч $AC$ параллелен оптической оси. После преломления в линзе он проходит через ее фокус $F$
- Луч $AO$ проходит через оптический центр $O$. После прохождения свозь линзу направление его распространения не изменяется
Эти два луча пересекутся в точке $A_1$. Эта точка является изображением точки $A$.
Точка $B$ лежит на оптической оси линзы. Мы можем построить ее изображение способом из прошлого урока, использую фокальную плоскость, побочную ось и побочный фокус. Но при построении изображения предмета, который располагается перпендикулярно оптической оси, мы можем сделать это проще. Для этого нам просто необходимо опустить перпендикуляр из полученной точки $A_1$ на оптическую ось. Так мы получаем изображение точки $B$ — $B_1$.
Если предмет будет располагаться под каким-то углом к оптической оси или обе его точки будут находиться не на оптической оси, необходимо выполнять построение изображения каждой точки предмета способами, описанными в прошлом уроке.
Теперь нам осталось соединить точки $A_1$ и $B_1$ между собой. Не перепутайте направление стрелки: если у предмета ее острие было в точке $A$, то у изображения предмета острие стрелки должно быть в точке $A_1$.
Характеристики изображения предмета
Итак, мы получили изображение предмета $A_1B_1$. Для того чтобы описать его, введем новые обозначения. Обозначим расстояние от предмета до линзы как $d$, а от линзы до изображения предмета как $f$.
Если $d > 2F$, то изображение предмета, даваемое собирающей линзой:
1. Действительное
2. Уменьшенное
3. Перевернутое
4. $F
Получим ли мы на практике точно такое же изображение? Возьмем большую собирающую линзу и свечу. Расположим свечу с помощью подставки таким образом, чтобы ее крайняя нижняя точка находилась на оптической оси (рисунок 3). Поместим ее за двойным фокусом линзы.
Передвигая экран ближе и дальше от линзы, найдем такое его положение, когда на нем появится изображение свечи. Мы увидим, что оно совпадаем с тем, которое мы получили на чертеже: уменьшенное, перевернутое и находится между фокусом и двойным фокусом линзы.
Настраивая фотоаппарат вручную, можно получить такое изображение.
Изображение предмета, находящегося между фокусом и двойным фокусом собирающей линзы
Будем постепенно приближать предмет к линзе. Теперь разместим его между фокусом и двойным фокусом линзы: $F Рисунок 4. Изображение предмета, находящегося между фокусом и двойным фокусом собирающей линзы
Построение изображения выполняется точно таким же образом, как и в прошлом случае. Отмечаем на чертеже ход двух лучей, выходящих из точки $A$. На их пересечении получаем точку $A_1$. Опускаем перпендикуляр на оптическую ось и отмечаем точку $B_1$. Соединяем две полученные точки между собой и получаем изображение предмета — $A_1B_1$. Охарактеризуем его.
Получается, что по мере приближения предмета к линзе (но не доходя до фокуса линзы), перевернутое изображение предмета будет удаляться от линзы, а его размеры будут увеличиваться.
Изображение предмета, находящегося перед фокусом собирающей линзы
Пододвинем предмет еще ближе к линзе. Теперь он находится между линзой и ее фокусом: $d Рисунок 5. Изображение предмета, находящегося между собирающей линзой и ее фокусом
Луч $AC$ преломляется после прохождения сквозь линзу и проходит через фокус. Мы получили преломленный луч $CC_1$.
Луч $AO$ проходит через оптический центр и не меняет своего направления. Из линзы выходит преломленный луч $OD$, совпадающий по направлению с падающим лучом.
Мы видим, что преломленные лучи $CC_1$ и $OD$ не пересекутся. Но если мы их продолжим в левую сторону чертежа, то получим точку пересечения — изображение точки $A$. Мы можем сразу сказать, что такое изображение будет мнимым, потому что пересекаются не сами преломленные лучи, а их продолжения.
Опустив перпендикуляр на оптическую ось, мы получим точку $B_1$. Соединим друг с другом точки $A_1$ и $B_1$, и изображение предмета $A_1B_1$ готово. Охарактеризуем его.
Если $d
Рисунок 6. Изображение предмета, даваемое рассеивающей линзой
Рассмотрим чертеж. Из точки $A$ выходят два луча $AC$ и $AO$. Луч $AC$ достигает линзы и преломляется. Луч $AO$ после прохождения сквозь линзу не изменяет своего направления.
Из чертежа сразу ясно, что преломленные лучи не пересекутся. Значит, должны пересечься их продолжения. Продолжение первого преломленного луча пройдет через мнимый фокус по определению рассеивающей линзы. Продолжение луча второго преломленного луча совпадает с лучом $AO$.
Эти продолжения пересекаются в точке $A_1$ — мнимом изображении точки $A$. Опустим перпендикуляр на оптическую ось и получим точку $B_1$. Соединим точки и получим изображение предмета $A_1B_1$.
Изображение, даваемое рассеивающей линзой:
1. Мнимое
2. Уменьшенное
3. Прямое
Подтвердим вышесказанное опытом. Возьмем большую рассеивающую линзу и свечу. Свечу установим на подставке так, чтобы ее крайняя нижняя точка находилась на оптической оси линзы (рисунок 7).
Смотря через линзу мы не увидим реальную свечу. Мы увидим ее мнимое, прямое и уменьшенное изображение $A_1B_1$. Все совпало с нашим чертежом.
Если мы начнем передвигать свечу относительно линзы, то увидим, что характеристики ее изображения будут сохраняться. Вне зависимости от положения свечи, ее изображение всегда будет мнимым, прямым и уменьшенным.
Выводы
Размеры и расположение изображения предмета в собирающей линзе зависят от положения предмета относительно линзы.
Рассеивающая линза дает уменьшенное, мнимое и прямое изображение, которое находится по ту же сторону от линзы, что и предмет. Оно не зависит от положения предмета относительно линзы.
Памятка построения изображений предмета
- Нарисуйте обозначение линзы и проведите ее оптическую ось. Отметьте оптический центр линзы
- Отметьте два фокуса линзы по обе стороны от нее. При этом фокусная длина выбирается произвольной, но одинаковой для обеих от линзы сторон
- Обозначьте на чертеже предмет там, где указано в задании
- Начертите ход двух лучей, исходящих от крайней точке предмета, если предмет перпендикулярен оптической оси и одна из точек расположена на ней.
- Если предмет находится под углом к оптической оси, или ни одна из точек не лежит на оптической оси, начертите ход двух лучей от каждой крайней точки предмета
- Используя точки пересечения лучей (или их продолжений), нарисуйте изображение предмета
- Охарактеризуйте его: действительное изображение или мнимое, прямое или перевернутое, его размеры и расположение относительно линзы
Пример построения изображения
Постройте изображение, которое даст собирающая линза, если предмет находится в двойном фокусе, как показано на рисунке 8.
Показать готовой чертеж и пояснения
При таком положении предмета нам нужно выполнить построение для каждой точки (рисунок 9).
Выберем два луча для точки $A$: $AC$ и $AO$. Луч $AC$ преломляется в линзе и после этого проходит через фокус линзы $F$. Луч $AO$ после преломления в линзе не меняет своего направления распространения. Эти преломленные лучи пересекутся в точке $A_1$.
То же самое проделаем с точкой $B$. Преломленные лучи пересекутся в точке $B_1$. Соединим полученные точки $A_1$ и $B_1$ — получим изображение предмета $A_1B_1$. Охарактеризуем его. (Напоминание: $d$ — это расстояние от предмета до линзы, $f$ — расстояние от изображения предмета до линзы).
Если $d = 2F$, то изображение предмета, даваемое собирающей линзой:
1. Действительное
2. Равного размера с предметом
3. Перевернутое
4. $f = 2F$
Источник