Учимся строить сечения многогранников. Часть 2.
Учимся строить сечения многогранников. Часть 2.
Эта статья для тех, кто хочет научиться строить сечения. Она содержит 11 заданий для построения сечений, подсказки и ответы к каждому заданию. Рекомендую сначала прочитать эту статью и посмотреть это видео.
Вспомним, что сечение многогранника плоскостью представляет собой плоский многоугольник, вершины которого принадлежат сторонам, а ребра — граням многогранника. Две соседние вершины принадлежат одной грани многогранника.
Чтобы найти точку, лежащую одновременно в двух плоскостях, нужно найти точку пересечения прямой, лежащей в первой плоскости, с прямой, лежащей во второй плоскости.
В подсказках и ответах изображение дополнительных прямых, используемых при построении сечения, сплошными линиями или пунктирными, не зависит от того, видимы эти прямые или нет.
Рядом с каждой дополнительной прямой указан ее порядковый номер при построении сечения. Все прямые проведены через две точки, принадлежащие определенной плоскости. Прямые пронумерованы в порядке их построения. Рекомендуется при использовании подсказки и воспроизведении построения сечения проговаривать, какой плоскости принадлежит данная прямая, каким плоскостям принадлежит точка их пересечения.
Постройте сечения, проходящие через точки 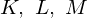
Задание 1:
Источник
Задачи на построение сечений многогранников.
Внимательно прочитайте условие выбранной задачи. Постройте чертёж многогранника и отметьте на нём заданные точки и линии. Постарайтесь представить требуемое сечение, а затем постройте его, пользуясь изученными аксиомами и теоремами из курса стереометрии. Только после этого имеет смысл открывать моё решение, чтобы сравнить его со своим. Не нужно сразу пугаться визуального несовпадения рисунков. Возможно, ваш многогранник просто развёрнут относительно моего, проверьте обозначения вершин. Главное – построение должно быть обоснованным, поэтому следите за блоком с теорией. Положения, которые я использовала при решении каждой из задач, будут выделены цветом.
Не забывайте, что плоскость сечения и сечение многогранника не совпадающие понятия. Плоскость бесконечна, а сечение — только часть этой плоскости.
Более того, в общем случае рассматриваемая плоскость может не пересекаться с многогранником вообще, иметь с ним только одну общую точку (вершину) или только один общий отрезок (ребро). В предлагаемых задачах школьного уровня сложности сечением многогранника является многоугольник, вершины которого лежат на рёбрах, а стороны на гранях многогранника.
Основные свойства плоскостей в пространстве
А1. Какова бы не была плоскость, существуют точки, принадлежащие этой плоскости, и точки, не принадлежащие ей.
А2. Если две различные плоскости имеют общую точку, то они пересекаются по прямой.
А3. Если две различные прямые имеют общую точку, то через них можно провести плоскость, и притом только одну.
Т1. Через прямую и не лежащую на ней точку можно провести плоскость, и притом только одну.
Т2. Если две точки прямой принадлежат плоскости, то вся прямая принадлежит этой плоскости.
Т3. Через три точки, не лежащие на одной прямой, можно провести плоскость, и притом только одну.
Параллельность прямых и плоскостей
Т4. Если прямая, не принадлежащая плоскости, параллельна какой-нибудь прямой в этой плоскости, то она параллельна и самой плоскости. (Признак параллельности прямой и плоскости.)
Т5. Две плоскости параллельны, если одна из них параллельна двум пересекающимся прямым, лежащим в другой плоскости. (Признак параллельности двух плоскостей.)
Т6. Через точку вне данной плоскости можно провести плоскость, параллельную данной, и притом только одну.
Т7. Если две параллельные плоскости пересекаются третьей, то прямые пересечения параллельны.
Т8. Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны.
Перпендикулярность прямых и плоскостей.
Т9. Если прямая, пересекающая плоскость, перпендикулярна двум прямым в этой плоскости, проходящим через точку пересечения, то она перпендикулярна плоскости. (Признак перпендикулярности прямой и плоскости.)
Т10. Если плоскость перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой.
Т11. Две прямые, перпендикулярные одной и той же плоскости, параллельны.
Т12. Прямая, проведенная на плоскости через основание наклонной перпендикулярно её проекции, перпендикулярна и самой наклонной. И обратно: если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна и проекции наклонной. (Теорема о трёх перпендикулярах.)
Т13. Если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны. (Признак перпендикулярности плоскостей.)
Т14. Если прямая, лежащая в одной из двух перпендикулярных плоскотей, перпендикулярна их линии пересечения, то она перпендикулярна и другой плоскости.
Понравились материалы сайта?
Узнайте, как поддержать сайт и помочь его развитию.
В условии не указано, что параллелепипед прямой, тем более прямоугольный, поэтому построение надо проводить для наиболее общего случая – наклонного параллелепипеда. Поскольку противолежащие грани параллелепипеда параллельны, то плоскость PQR пересекает грань CDD1C1 по линии FE || PQ (Т7).
Чтобы построить требуемую линию пересечения, продолжаем прямые, принадлежащие двум другим боковым граням параллелепипеда до пересечения с продолжениями рёбер основания. Таким образом находим общие точки плоскостей PQR и ABC (А2). Осталось соединить найденные точки прмой линией MN.

Через каждую точку, из которой требуется опустить перпендикуляр, и прямую A1Q проходит плоскость (Т1). Строим эти плоскости. Поскольку в задаче не требовалось построить полностью сечения параллелепипеда, то для каждого случая достаточно соединить три точки отрезками попарно.
В получившихся треугольниках строим соответствующие высоты. Это и есть искомые перпендикуляры.
Трудность состоит в том, что на объёмном чертеже искажается реальный тип треугольника: остроугольный, прямоугольный или тупоугольный. Поэтому неясно, куда в итоге попадает основание перпендикуляра: на противоположную вершине сторону, в край отрезка или на её продолжение. Поэтому нужно определить относительные длины сторон треугольников, что легко сделать применяя теорему Пифагора к прямоугольным треугольникам на гранях параллелепипеда.
Длины сторон будем «измерять» в частях. Тогда
AB = 1; AD = 3; AA1 = 1; BQ = 2.
Из треугольника ABQ получим: AQ = √ 5 __
Из треугольника AА1Q получим: A1Q = √ 6 __
Из треугольника ADА1 получим: DA1 = √ 10 ___
Осталось сделать плоские чертежы в масштабе или, что лучше, применить теорему косинусов для определения углов треугольников, но этот способ мы рассмотрим с заданиями по планиметрии.
Обратите внимание — для лучшего визуального восприятия параллепипед на нижнем чертеже развёрнут относительно верхнего.
Строим PR || AC (Т4). Точки P и R расположены на рёбрах призмы, каждая из них принадлежит двум граням призмы и плоскости сечения. Чтобы найти еще такие точки, но принадлежащие другим граням, продолжаем содержащие эти точки прямые до пересечения. AB пересекается с PR в точке M и BC пересекается с PR в точке N. Соединяя Q с M и Q с N, получим недостающие прмые, принадлежащие боковым граням призмы (А2). Пятиугольник RFQEP – искомое сечение.
Эта задача аналогична 5-ой. Только с разворотом.
Отличается от заданий 5 и 11 только пропорциями пирамиды. Нужно рассмотреть плоский треугольник AMC, чтобы определить положение точки Н на прямой МС.
Чтобы построить сечение плоскостью, перпендикулярной заданной прямой, нам, как всегда, нужно опустить на эту прямую два пересекающихся перпендикуляра (Т9). Здесь три грани пирамиды являются равными равнобедренными прямоугольными треугольниками, и одна грань (ASB) – равносторонним треугольником. На плоских чертежах этих треугольников хорошо видно, где будут расположены концы перпендикуляров.
Строим: PR ⊥ SA, затем RN ⊥ SA, P и N соединяем.
Случай B. Требуемая плоскость сечения строится аналогично. Однако в этом случае прямая LЕ || B1F пересеклась не со стороной BD параллелограмма ВВ1D1D, которая принадлежит плоскости основания призмы, а со стороной D1D, которая является боковым ребром вспомогательного параллелепипеда. Поэтому нужно применить приём продолжения отрезков прямых, лежащих в одной плоскости, но принадлежащих также другим плоскостям, до пересечения. Здесь отрезки BD и LE расположены в плоскости ВВ1D1D, их продолжения пересекаются в точке О этой плоскости. Но отрезок BD является ребром призмы, поэтому принадлежит также плоскости её основания, а отрезок LE принадлежит также плоскости сечения, поэтому точка О — общая точка плоскости основания и плоскости сечения. Осталось соединить точки H и О (А2, Т2). HLO — плоскость сечения призмы, треугольник HLR — искомое сечение.
Это, фактически, только ответ. Подробное решение в другом разделе: Две задачи на построение сечений.
Чтобы опустить перпендикуляр из точки на прмую, нужно найти плоскость, в которой это можно сделать, т.е. плоскость, проходящую через эту точку и заданную прямую (Т1). Здесь такая плоскость строится легко, это сечение SDE. Искомый перпендикуляр ‐ высота EH в треугольние SDE. Плоский рисунок и соотношения длин отрезков в пирамиде нужны для того, чтобы уточнить положение точки Н.
Внимание: Если вы нашли ошибку или опечатку, пожалуйста, сообщите о ней на email.
Есть вопросы? пожелания? замечания? Обращайтесь — mathematichka@yandex.ru
Внимание, ©mathematichka. Прямое копирование материалов на других сайтах запрещено.
Источник