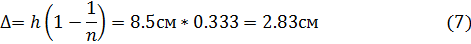Как найти увеличение системы собирающих линз
Во многих оптических приборах свет последовательно проходит через две или несколько линз. Изображение предмета, даваемое первой линзой, служит предметом (действительным или мнимым) для второй линзы, которая строит второе изображение и т. д. Таким образом, расчет оптической системы из двух или нескольких линз сводится к последовательному применению формулы линзы. При этом расстояние от первого изображения до второй линзы следует положить равным величине , где – расстояние между линзами.
Общее линейное увеличение системы из двух линз равно произведению линейных увеличений обеих линз
| . |
Если предмет или его изображение находятся в бесконечности, то линейное увеличение системы из двух линз теряет смысл.
Компьютерная модель предназначена для изучения системы из двух линз. Можно изменять положение обеих линз относительно предмета либо с помощью соответствующих контролов, либо непосредственно с помощью мыши. В широких пределах можно изменять оптические силы () обеих линз. Компьютер вычисляет положения первого и второго изображений и определяет линейные увеличения системы из двух линз и каждой линзы в отдельности. Точечный предмет располагается на общей оптической оси линз. На дисплее высвечивается ход двух произвольных лучей от предмета, испытывающих преломление в обеих линзах.
Обратите внимание, что в том случае, когда второе изображение предмета находится в бесконечности (), система из двух линз моделирует ход лучей в микроскопе в предположении, что глаз наблюдателя аккомодирован на бесконечность.
Источник
Линейное увеличение в линзах
Ещё одним параметром, характеризующий систему из линз и сферических зеркал, является линейное увеличение.
Линейным увеличением называется отношение высоты получившегося изображения к высоте предмета:
- где
- Г — линейное увеличение,
- — высота получившегося изображения,
- — высота исходного предмета.
Вопрос о поиске данного параметра может возникнуть и в задачах на построение , и в задачах на формулы тонкой линзы и сферического зеркала.
Пусть даны предмет, линза и изображение предмета в линзе (рис. 1).
Рис. 1. Линейное увеличение
При построении мы использовали луч от предмета ( ), который проходит через главный оптический центр линзы (при этом не преломляясь). При этом у нас получились два подобных треугольника (подобие по трём углам). Тогда, используя подобие, можем записать:
- где
- — расстояние от предмета до линзы,
- — расстояние от изображения до линзы.
Вывод: вопросы, связанные с линейным увеличением, решаются или через логику построения в системах (рис.1), или через соотношение (2) при наличии численных значений параметров линз.
Источник
Определить увеличение, даваемое системой линз
Прохождение гомоцентричного пучка света через плоскопараллельную пластинку.
| Рисунок 1 |
ПП пластинка с коэффициентом преломления, отличным от показателя преломления среды, не изменяет направление луча, она лишь смещает его параллельно самому себе. Если на пластинку падает гомоцентричный пучок лучей, то при небольших углах падения – α, если tg (α)≈sin(α), гомоцентричность сохраняется. Однако кажущийся центр пучка смещается вдоль оси пучка. В случае сходящегося пучка его центр удаляется от пластинки на расстояние Δ, а, в случае расходящегося пучка – приближается к пластинке на то же расстояние.
Вычислим величину Δ согласно рисунку.
Подставим AB-CD в формулу для Δ:
Δ=d- d*tg(β) ctg(α)=d(1- tg(β)/tg(α)) Для малых углов отношение тангенсов заменяется отношением синусов, а отношение синусов – относительным показателем преломления – n. В результате получим.
Исходные данные варианта приведены в таблице, а расположение элементов на рисунке 2.
| R1, м | R2, м | R3, м | R4, м | һ, см | a1, см | a2, см | b, см | Тип билинзы | ε, мм | λ, нм |
| 0,25 | 0,55 | 0,65 | 0,85 | 8,5 | 6,5 | 4,5 | 6б | 0,25 |
| Рисунок 2 |
Решение:
Найти фокусные расстояния и оптические силы линз Вашей оптической системы
• Формула, определяющая оптическую силу:
• 
• Где R1, R2 – радиусы кривизны соответственно левой и правой поверхностей линзы. Радиус положителен, если центр кривизны правее центра линзы. Радиус отрицателен, если центр кривизны левея центра линзы.
• Для линзы 1 
Фокусные расстояния f1=1/D=0.273 м
Для линзы 3 
Фокусные расстояния f3=1/D=-0.578 м.
Пункт 1 выполнен.
2. Найти положение изображения источника.
Источник света находится на расстоянии 65 см от первой линзы, у которой фокусное расстояние f=23.7 см. Поскольку предмет находится на расстоянии, превышающем двойное фокусное расстояние собирающей линзы, изображение будет действительным перевернутым и уменьшенным. Расходящийся пучок света от источника после прохождения первой линзы станет сходящимся. Поместим начало координат в центр первой линзы. Координата источника xs=-0.65 м. Если пока не учитывать действие плоскопараллельной пластинки, то координата изображения источника – xs’, даваемого первой линзой определится из формулы линзы:
Плоскопараллельная пластинка, получая сходящийся пучок лучей, отдалит точку схождения пучка на расстояние
В результате координата изображения источника, даваемого первой линзой и пластинкой, будет равна:
Перенесем начало координат в центр второй линзы и будем считать изображение источника первой линзой предметом для второй линзы. Для различения систем координат для первой и второй линз обозначим координаты для второй линзы буквой z. Тогда координата предмета для второй линзы будет равна:
Координата изображения, даваемого второй линзой, определится формулой (6) с заменой обозначений. Учтем также, что вторая линза – рассеивающая и ее фокусное расстояние отрицательною
Изображение получается справа от второй линзы, т.е является действительным.
Пункт 2 выполнен.
Определить увеличение, даваемое системой линз
Увлечение, даваемое системой линз, равно произведению увеличений, даваемых каждой из линз системы: Г=Г1*Г2
Формула для поперечного увеличения одиночной линзы:
Где f – фокусное расстояние линзы, xs – координата предмета.
Изображение в первой линзе получается уменьшенным, перевернутым
Хоть линза и рассеивающая, но изображение дает действительное, увеличенное, не перевернутое.
Общее увеличение системы из двух линз:
Изображение действительное перевернутое, увеличенное.
Пункт 3 выполнен.
4.
| Рисунок 3 |
В системе оставляют одну собирающую линзу (если их в системе две, то любую по Вашему выбору). Из этой линзы делают билинзу Бийе путем распиливания по диаметру на две половины и: сдвиганием или раздвиганием частей симметрично относительно оси на расстояние ε. Два возможных варианта билинзы показаны на рисунке.
Источник монохроматического света с длиной волны λ находится на оси симметрии билинзы. Задавая самостоятельно расстояние от источника до билинзы и расстояние от билинзы до экрана, перпендикулярного оси симметрии, найти ширину интерференционных полос на экране и количество полос на экране.
Положение источника света необходимо задать так, чтобы световые потоки от него после прохождения верхней и нижней полулинз затем пересекались. Для этого при использовании раздвижной билинзы источник должен находится от линзы дальше ее фокальной плоскости, а в случае сдвижной билинзы — ближе.
На рисунке 4 показаны области пересечения световых потоков в обоих случаях. Эта область заключена между лучами, проходящими от источника через оптические центры полулинз (точки О1, О2). В случае раздыижной билинзы эти центры находятся на линии разреза, в случае сдвижной билинзы оптические центры сошлифованы и являются воображаемыми.
Для расчета ширины интерференционных полос можно полагать, что свет исходит из двух вторичных когерентных источников S1 и S2. В случае раздвижной билинзы эти источники являются действительными изображениями, которые дают половинки билинзы, а в случае сдвижной изображения источника являются мнимыми.
Источник
