Что такое полюс сечения сопромат

Техническая механика

Сопротивление материалов

Геометрические характеристики плоских сечений

При некоторых видах деформаций прочность и жесткость (способность противостоять деформации) элементов конструкций зависит не только от величины поперечного сечения, но и от формы этого сечения.
Самый простой пример — обыкновенную школьную линейку можно легко изогнуть относительно широкой стороны поперечного сечения и совершенно невозможно изогнуть относительно его короткой стороны. При этом общая площадь сечения в обоих случаях одинакова. На основании этого примера становится очевидным, что на сопротивление некоторым видам деформации оказывает влияние (иногда — решающее) не только величина площади сечения бруса, но и его геометрическая форма.
При изучении деформаций изгиба и кручения нам потребуется знание некоторых геометрических характеристик плоских сечений, которые оказывают влияние на способность конструкций сопротивляться деформациям относительно той или иной оси либо полюса (точки).

Чтобы понять суть явления и влияния этих геометрических характеристик на сопротивление бруса, например, изгибу, следует обратиться к основополагающим постулатам сопромата. Как известно из установленного в 1660 году английским физиком Робертом Гуком закона, напряжение в сечениях бруса прямо пропорционально его относительному удлинению. Очевидно, что волокна, расположенные дальше от оси изгиба, растягиваются (или сжимаются) сильнее, чем расположенные вблизи оси. Следовательно, и напряжения возникающие в них будут бόльшими.
Можно привести условную сравнительную аналогию между напряжением в разных точках сечения бруса с моментом силы — чем больше плечо силы — тем больше ее момент (относительно оси или точки). Аналогично — чем дальше от какого-либо полюса (оси) отстоит точка в сечении, тем большее напряжение в ней возникает при попытке изогнуть или скрутить брус относительно этого полюса (оси).

Статический момент площади

Статическим моментом площади плоской фигуры относительно оси, лежащей в той же плоскости, называется взятая по всей площади сумма произведений элементарных площадок (S_i) на расстояния (r_i)от них до этой оси.

Если упростить это определение, то статический момент инерции плоской фигуры относительно какой-либо оси (лежащей в той же плоскости, что и фигура) можно получить следующим образом:

• разбить фигуру на крохотные (элементарные) площадки (рис. 1);
• умножить площадь каждой площадки на расстояние r_i от ее центра до рассматриваемой оси;
• сложить полученные результаты.

Статический момент площади плоской фигуры обозначают S с индексом оси, относительно которой он рассматривается: S_x , S_y , S_z .

Примечание: в разных учебниках или других источниках информации обозначение тех или иных физических величин может отличаться от приведенных на этом сайте. Как вы понимаете, от условного обозначения величин суть описываемых явлений и закономерностей не изменяется.

Анализ этих формул позволяет сделать вывод, что статический момент площади фигуры относительно оси, лежащей в этой же плоскости, равен произведению площади фигуры на расстояние от ее центра тяжести до этой оси.
Из этого вывода следует еще один вывод — если рассматриваемая ось проходит через центр тяжести плоской фигуры, то статический момент этой фигуры относительно данной оси равен нулю.

Единица измерения статического момента площади — метр кубический (м 3 ).
При определении статического момента площади сложной фигуры можно применять метод разбиения, т. е. определять статический момент всей фигуры, как алгебраическую сумму статических моментов отдельных ее частей. При этом сложная геометрическая фигура разбивается на простые по форме составные части — прямоугольники, треугольники, окружности, дуги и т. п., затем для каждой из этих простых фигур подсчитывается статический момент площади, и определяется алгебраическая сумма этих моментов.

Полярный момент инерции

Полярным моментом инерции плоской фигуры относительно полюса (точки), лежащего в той же плоскости, называется сумма произведений элементарных площадок (S_i) этой фигуры на квадрат их расстояний (r 2 _i) до полюса.
Полярный момент инерции обозначают I_ρ (иногда его обозначают J_ρ ), а формула для его определения записывается так:

Единица измерений полярного момента инерции — м 4 , из чего следует, что он не может быть отрицательным.
Понятие полярного момента инерции понадобится при изучении деформаций кручения круглых валов, поэтому приведем формулы для определения полярного момента квадратного, круглого и кольцевого сечения.

Источник

Глава 1. Геометрические характеристики плоских сечений

1.1. Понятие о геометрических характеристиках сечения

Для оценки прочности инженерных конструкций в курсе сопротивления материалов и механики деформируемого твёрдого тела изучают связи между силами, действующими на элементы конструкции и деформациями. Основные задачи — расчёт элементов конструкций на прочность, жёсткость и устойчивость. Эти задачи решают не в любой, а в специально выбранной главной, центральной системе координат с использованием специфических геометрических характеристик поперечных сечений элементов конструкций.

Рассмотрим два положения стержня, жестко закреплённого одним торцом (рис 1.1):

F

F

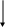
Стержень нагружен силой F, проходящей через центр тяжести незакрепленного сечения. Очевидно, что в первом случае стержень выдержит большую нагрузку, хотя площади сечений и длины стержней одинаковы. Следовательно, для оценки прочности, жесткости и устойчивости стержня помимо площади сечения необходимы какие-то дополнительные геометрические характеристики сечения.

К этим геометрическим характеристикам относят статические моменты сечения, осевые, полярный и центробежный моменты инерции сечения.

1.2. Статические моменты сечения

Рассмотрим сечение произвольной формы и введем декартовую систему координат (рис.1.2).

Y

dA

y

x X

Статическим моментом сечения относительно оси х называют величину S_x , определяемую по формуле

(1.1)

где у – ордината текущей точки сечения; dA – элементарная площадка плоского сечения, имеющего площадь А; dA и А считаем положительными.

Аналогично определяют статический момент S_y:

. (1.2)

Заметим, что: 1) правая часть равенств (1.1) и (1.2) представляют собой поверхностные интегралы первого типа и интегрирование выполняется по всей площади сечения; 2) единицы измерения величин, S_x и S_y — м 3 , у – м, dA – м 2 ; 3) знаки величин S_x и S_y зависят от положения осей х и у соответственно (например, ось х ниже сечения S_x > 0; ось х выше сечения S_x 4 ; 2) подинтегральные выражения в равенствах (1.9), (1.10), (1.12) – неотрицательны. Значит осевые , и полярный моменты всегда положительны, хотя их величины зависят от выбранной системы координат. Знак и величина центробежного момента зависят от выбранной системы координат. Например, на рис. 1.4 для всех точек сечения х>0, y>0 и >0, а на рис. 1.5 x 0 и 1 / 7 1234567> Следующая >>>

Читайте также:  Дифракционная решетка с линзой задачи

Источник