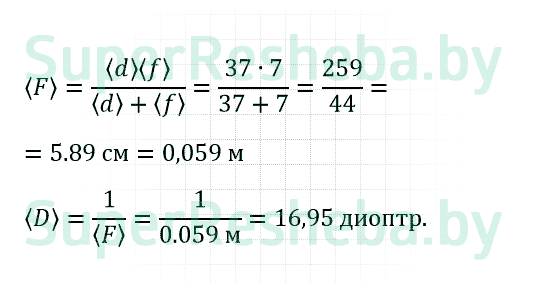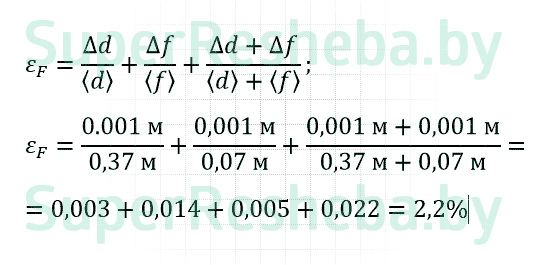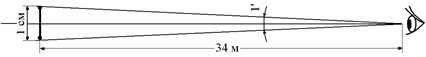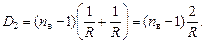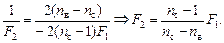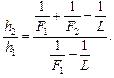Системы линз
Некоторое количество задач школьной физики связаны с построением изображений или использованием формулы тонкой линзы для систем, состоящих из нескольких линз. Все эти системы центрированы, т.е. главные оптические оси линз совпадают.
Для таких систем важно правильно прочитать условие задачи. Выделяют два способа соединения линз в систему:
- линзы, стоящие вплотную,
- линзы, стоящие далеко друг от друга
Для линз, стоящих вплотную, используется достаточно простая логика: оптическая сила составной линзы есть сумма оптических сил каждой из линз, входящих в систему. Или формульно:
- где
- — оптическая сила составной линзы,
- — сумма оптических сил линз, входящих в систему.
Важно: необходимо помнить о знаках оптической силы. Так, если линза собирающая, то её оптическая сила положительна, если линза рассеивающая, то её оптическая сила отрицательна.
Для линз, разнесённых на расстояние превышающее двойное фокусное, логика немного другая. Для таких систем:
- будем считать линзы и построение в них не зависящими друг от друга (т.е. при построении лучи, преломлённые в одной линзе, не «видят» другой линзы до нахождения изображения).
- изображение, полученное в первой линзе, будет являться предметом для второй линзы.
Пусть даны две собирающие линзы с фокусными расстояниями и соответственно.
Мы уже знаем как строить изображения в каждой из них. От предмета мы получаем изображение в первой линзе , не взирая на вторую линзу. Затем, не смотря уже на первую линзу, ищем изображение как предмета во второй линзе и получаем . Таким образом, друг за другом, мы можем получить изображение изначального предмета во сколь угодно большом количестве линз.
Вывод: для систем линз важно выяснить, как расположены линзы (вплотную или разнесены), и выбрать метод решения (уравнение (1) или рис. 1).
Источник
Лаб. 6
ΔF = ε · = 0.022 · 0.059 м = 0,0013 м
| № | d | Δd | f | Δf | F | D | ε | ΔF |
| 1 | 0,37 | 0,001 | 0,07 | 0,001 | 0,059 | 16,95 | 2,2 | 0,0013 |
| 2 | 0,37 | 0,001 | 0,07 | 0,001 | ||||
| 3 | 0,37 | 0,001 | 0,07 | 0,001 | ||||
| 4 | 0,37 | 0,001 | 0,07 | 0,001 | ||||
| 5 | 0,37 | 0,001 | 0,07 | 0,001 | ||||
| Ср. | 0,37 | 0,001 | 0,07 | 0,001 | 0,059 | 16,95 | 2,2 | 0,0013 |
1. В каком случае линзу можно считать тонкой?
Если она имеет два симметрично расположенных фокуса, через которые проходят параллельные пучки лучей (или их продолжений) после преломления в линзе.
2. Как по внешним признакам отличить собирающую линзу от рассеивающей?
Собирающая линза является выпуклой, а рассеивающая – вогнутой.
Выводы: Линза с F > 0 является собирающей, а линза с F —>
Закройте тёмной бумагой половину линзы и опишите, как при этом изменится изображение предмета на экране?
Размеры и ориентация изображения не изменятся, так как линза до сих пор присутствует, но изменится яркость изображения, так как количество лучей, проходящих через линзу изменится.
Источник
Близорукость и дальнозоркость
Глаз. Угол зрения. Очки
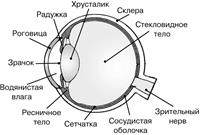 Рис. 10.1 Рис. 10.1 |
Как устроен глаз?
Глаз человека имеет почти шарообразную форму (рис. 10.1). Его диаметр около 2,5 см. Снаружи глаз покрыт защитной оболочкой белого цвета – склерой. Передняя прозрачная частьсклеры называется роговой оболочкой или роговицей. С внутренней стороны к склере прилегает сосудистая оболочка, состоящая из сложного сплетения кровеносных сосудов, питающих глаз. Эта вторая оболочка в передней части глаза переходит в радужную оболочку, окрашенную у разных людей в различный цвет. В радужной оболочке имеется отверстие – зрачок. В зависимости от интенсивности падающего света диаметр зрачка рефлекторно меняется приблизительно от 2 до 8 мм. За зрачком помещается хрусталик – прозрачное слоистое тело, похожее на линзу. Особая мышца – ресничное тело – может в некоторых пределах менять форму хрусталика, делая его более выпуклым при рассматривании близких предметов.
Между роговицей и радужной оболочкой находится водянистая жидкость. Остальную часть глаза до задней стенки (глазного дна) занимает прозрачное полужидкое стекловидное тело. Глазное дно покрыто очень сложной сетчатой оболочкой (сетчаткой), представляющей собой разветвления зрительного нерва с нервными окончаниями в виде палочек и колбочек. Палочки и колбочки являются светоощущающими элементами.
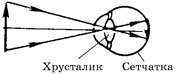 Рис. 10.2 Рис. 10.2 |
В то же время принципиальная оптическая схема глаза достаточно проста и состоит из двух основных элементов: собирающей линзы и экрана. Собирающей линзой в глазу служит хрусталик,а экраном – сетчатка (рис. 10.2).
Назначение хрусталика такое же, как и у объектива фотоаппарата, – создавать действительные перевернутые изображения наблюдаемых предметов. Эти изображения получаются на сетчатке. Сетчатка образует светочувствительную поверхность глаза, ее назначение такое же, как у фотопластинки в фотоаппарате. Разница только в том, что изображение, полученное на фотопластинке, проявляется в фотолаборатории при помощи химических процессов, а изображение, полученное на сетчатке, по нервным волокнам передается в мозг, где оно при помощи биологических процессов мгновенно «проявляется», и в человеческом сознании возникают зрительные образы.
Но для того, чтобы в нашем сознании возник четкий зрительный образ наблюдаемого предмета, необходимо, чтобы изображение предмета получилось точно на сетчатке. В фотоаппарате при наводке на резкость перемещают объектив, изменяя тем самым расстояние от линзы до экрана. В человеческом глазу наводка на резкость осуществляется по-другому: глазные мышцы способны изменять форму хрусталика, а значит, и его оптическую силу. Когда мы переводим взгляд на различные предметы, глазная мышца «автоматически» обеспечивает наводку на резкость, то есть придает хрусталику такую форму, чтобы изображение рассматриваемого предмета получалось точно на сетчатке. Способность глаза к видению на близком и дальнем расстоянии называется аккомодацией.
Если глазная мышца полностью расслаблена, то глаз «настроен» на бесконечность, то есть параллельный пучок лучей, попадающий в глаз, собирается в точку точно на сетчатке. При такой «настройке» на сетчатке получаются четкие изображения сильно удаленных предметов. Именно поэтому, когда человек хочет дать глазам отдых, он смотрит вдаль (рис. 10.3,а).
Чем ближе к глазу рассматриваемый предмет, тем сильнее должен хрусталик преломлять идущие на него лучи, чтобы изображение получилось на сетчатке (рис. 10.3,б). А это значит, что чем ближе предмет, тем больше должна быть оптическая сила хрусталика, тем сильнее должна быть напряжена глазная мышца.
Но возможности глазной мышцы не безграничны: настроить хрусталик на рассматривание предметов, расположенных ближе 10–12 см от глаза глазная мышца уже не в силах. При слишком малых расстояниях от предмета до глаза даже при максимально возможной оптической силе хрусталика изображение предмета получается за сетчаткой (рис. 10.3,в).
На самой же сетчатке в этом случае (а значит, и в человеческом сознании) возникает нечеткое, размытое изображение предмета.
СТОП! Решите самостоятельно: В4, С1, С2.
Для нормального глаза наиболее благоприятным для рассматривания предметов оказывается расстояние примерно в 25 см. При таком расстоянии глаз достаточно хорошо различает детали и не слишком утомляется, именно на таком расстоянии от глаз держит книгу человек с нормальным зрением. Это расстояние называется расстоянием наилучшего зрения.
Задача 10.1. Человек читает книгу, держа ее на расстоянии d1 = = 25 см от глаз. На сколько надо изменить оптическую силу хрусталика, чтобы читать книгу на расстоянии d2 = 20 см от глаз?
| d1 = 25 см d2 = 20 см | Решение. Запишем формулу линзы для обоих случаев: 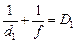 , (1) , (1) 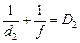 . (2) . (2) |
| DD = ? |
Здесь d1 и d2 – расстояния от книги до глаза; f – расстояние от хрусталика до сетчатки (человеческий глаз устроен так, что это расстояние меняться не может); D1 и D2 – оптические силы хрусталика в первом и втором случаях соответственно. Мы должны найти величину DD = D2 – D1.
Вычтем из уравнения (2) уравнение (1) и получим:
DD = D2 – D1 = 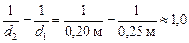
Ответ: DD = 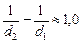
СТОП! Решите самостоятельно: А3, В5, В6.
Угол зрения
Читатель: Когда рассматриваешь два небольших предмета на большом расстоянии, то они как бы сливаются в один. Почему это так?
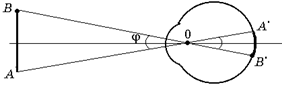
Автор: Дело в том, что сетчатка состоит из отдельных светочувствительных элементов. Допустим, два маленьких предмета расположены настолько близко друг к другу, что их изображения на сетчатке получились на одном и том же светочувствительном элементе. В этом случае два предмета будут восприниматься как одна точка. Чем больше величина изображения А¢В¢ на сетчатке глаза, тем больше светочувствительных элементов участвует в восприятии предмета АВ, а значит, тем больше подробностей этого предмета мы можем различать (рис. 10.4).
Как видно из рисунка, величина изображения предмета в глазу определяется отнюдь не размерами предмета, а углом, под которым мы видим данный предмет. На рис. 10.4 – это угол j.
Угол, образованный прямыми, проведенными от краев предмета в оптический центр глаза, называется углом зрения.
Именно от угла зрения, а не от размеров предмета зависит на сколько светочувствительных элементов сетчатки будет попадать свет от данного предмета. Поэтому очень большие предметы, расположенные очень далеко, например Луна, кажутся нам не больше мелкой монеты, которую мы держим в руке.
Нормальный глаз плохо различает детали предмета, который он видит под углом менее 1¢ (это угол, под которым виден отрезок длиной 1 см с расстояния 34 м, рис. 10.5). Приближая предмет к глазу, мы увеличиваем угол зрения и, следовательно, получаем возможность лучше рассматривать мелкие детали.
СТОП! Решите самостоятельно: А1, В1.
Задача 10.2. На каком расстоянии друг от друга должны находиться два человека, чтобы глаз смог различить их с расстояния около 11 км? Разрешающая способность нормального глаза составляет примерно 1¢.
| l = 11 км j = 1¢ | Решение. Сначала заметим, что 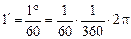 рад » 2,91×10 –4 рад. Рассмотрим рис. 10.6. рад » 2,91×10 –4 рад. Рассмотрим рис. 10.6. |
| х = ? |
Как видно из рисунка, 
СТОП! Решите самостоятельно: А2, В2, В3.
Составная линза
Возьмем две тонкие линзы с оптическими силами D1 и D2 и расположим их вплотную друг к другу, как показано на рис. 10.7.
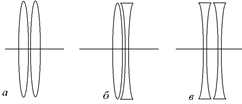
При этом линзы могут быть как собирающими, так и рассеивающими. Попробуем ответить на вопрос: линзу с какой оптической силой надо взять, чтобы она смогла заменить данную пару линз? То есть чтобы она преломляла падающие на нее лучи точно так же, как пара линз.
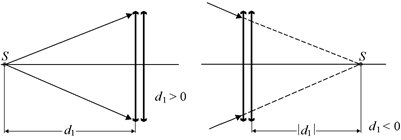
Расположим перед парой линз источник света на расстоянии d от их оптического центра (толщиной линз пренебрегаем). Источник света S может быть как действительным (рис. 10.8, а), так и мнимым (рис. 10.8, б).
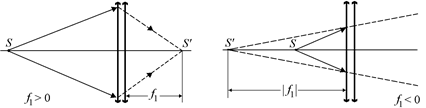
Если бы не было второй линзы, то лучи, прошедшие через первую линзу, дали бы изображение в точке S¢. Это изображение могло бы быть как действительным (рис. 10.9, а), так и мнимым (рис. 10.9, б).
Читатель: Но на пути лучей, преломившихся в первой линзе, стоит вторая линза!
Автор: Верно! И эта вторая линза воспринимает лучи, прошедшие через первую линзу, так, как если бы эти лучи исходили из действительного источника, расположенного в точке S¢ (см. рис. 10.9, б), или из мнимого источника, расположенного в точке S¢ (см. рис. 10.9, а).
Читатель: То есть получается, что если первая линза дает мнимое изображение, то вторая линза «воспринимает» это мнимое изображение как действительный источник, а если первая линза дает действительное изображение, то вторая линза его «воспринимает» как мнимый источник?
Автор: Совершенно верно! Поэтому если для первой линзы формула линзы имеет вид
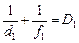
то для второй линзы формула линзы имеет вид
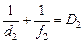
В самом деле, если f1 > 0 (см. рис. 10.9, а), то d2 0 и S¢– действительный источник для второй линзы. Тогда уравнение (2) можно записать так:

Теперь сложим почленно уравнения (1) и (3), получим
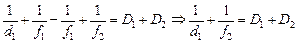
Здесь f2 – расстояние от оптического центра до изображения, взятое с учетом знака.
Получается, что система линз «работает» точно так же, как одна линза с оптической силой
Читатель: А если линз будет больше, например, три?
Автор: Тогда мы можем повторить наши рассуждения, рассматривая первые две линзы как одну с оптической силой D12 = D1 + D2. Ясно, что оптическая сила трех линз будет равна D = D12 + D3, то есть
Но если мы возьмем слишком много линз, например 100, то наши рассуждения потеряют силу, так как при таком количестве линз составная линза будет слишком «толстой». А все наши рассуждения годятся только для случая, когда толщиной составной линзы можно пренебречь по сравнению с ее фокусным расстоянием.
Задача 10.3. Две одинаковые плосковогнутые линзы, сложенные плоскими сторонами, образуют линзу с фокусным расстоянием F1. Найти фокусное расстояние F2 линзы, которая получится, если сложить эти линзы вогнутыми сторонами, а пространство между ними заполнить водой. Показатели преломления стекла и воды равны пс = 1,66, пв = 1,33.
| F1 пс = 1,66 пв = 1,33 | Решение. Пусть R – радиус сферической поверхности плосковогнутой линзы (рис. 10.10). Тогда фокусное расстояние F одной такой линзы можно найти по формуле 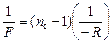 . (1) Если сложить две таких линзы плоскими сторонами, то их оптическая сила согласно формуле (10.1) будет равна . (1) Если сложить две таких линзы плоскими сторонами, то их оптическая сила согласно формуле (10.1) будет равна |
| F2= ? | |
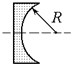 Рис. 10.10 Рис. 10.10 | |
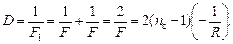 (2) Если сложить две тонких линзы вогнутыми сторонами, а пространство между ними заполнить водой, то получится система уже из трех линз (рис. 10.11). (2) Если сложить две тонких линзы вогнутыми сторонами, а пространство между ними заполнить водой, то получится система уже из трех линз (рис. 10.11). | 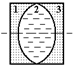 Рис. 10.11 Рис. 10.11 |
Оптическая сила линз 1, 2 и 3 соответственно равна:
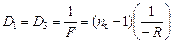
Общая оптическая сила системы линз по формуле (10.2) равна
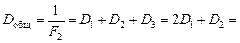

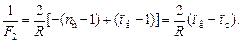
Выразим величину R из формулы (2) и подставим в (3):
Подставим численные значения:
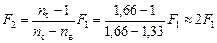
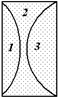 Рис. 11.12 Рис. 11.12 |
Ответ: 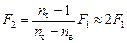
СТОП! Решите самостоятельно: А4, В7, С3.
Задача 10.4. Из стеклянной пластинки изготовлены три линзы (рис. 10.12). При этом оказалось, что оптическая сила системы (1, 2) равна –2 дптр, а оптическая сила системы (2, 3) равна –3 дптр. Найти оптическую силу линзы 2.
| D12 = –2 дптр D23 = –3 дптр | Решение. По условию задачи D1 + D2 = –2 дптр, (1) D2 + D3 = –3 дптр. (2) |
| D2 = ? |
Кроме того, все три линзы образуют плоскопараллельную пластину, а оптическая сила плоскопараллельной пластины равна нулю. Тогда
Выразим из формулы (1) D1, из (2) D3 и подставим в (3):
СТОП! Решите самостоятельно: А5, В8, С4.
Задача 10.5. Проекционный аппарат, объектив которого имеет фокусное расстояние F1, установлен на расстоянии L от экрана. Во сколько раз изменится размер изображения, если на объектив надеть насадочную собирающую линзу с фокусным расстоянием F2?
| F1 F2 L | Решение. В первом случае (рис. 10.13, а) формула линзы имеет вид 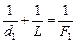 . (1) . (1) |
| h2/h1 = ? |
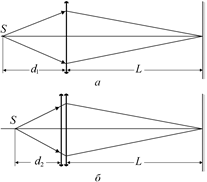 Рис. 10.13 Рис. 10.13 |
Во втором случае (рис. 10.13, б)
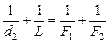
Пусть размер предмета h, а размеры изображения в первом и во втором случаях соответственно равны h1 и h2. Тогда линейное увеличение объектива в первом и втором случаях соответственно равно:
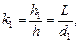
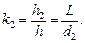
Разделим уравнение (4) на уравнение (3), получим:
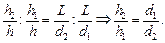
Нам осталось найти отношение 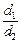
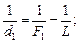
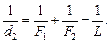
Чтобы найти искомое отношение 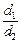
Согласно уравнению (5) это выражение и является ответом.
Ответ:
СТОП! Решите самостоятельно: В9, С5, D1.
Близорукость и дальнозоркость
При близорукости человек может хорошо рассматривать только близко расположенные предметы. Предметы, расположенные далеко, он видит лишь «в общих чертах», их очертания представляется ему размытыми.
При дальнозоркости же человек, наоборот, хорошо видит удаленные предметы (хоть и не лучше, чем человек с нормальным зрением), но зато близко расположенные предметы он видит плохо. Например, читать книгу дальнозоркому человеку очень трудно: чтобы хоть как-то разобрать текст, он должен держать книгу достаточно далеко от себя, а на большом расстоянии буквы трудно хорошо рассмотреть.
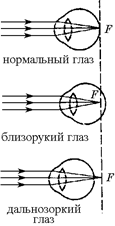 Рис. 10.14 Рис. 10.14 |
В чем же причина этих широко распространенных недостатков зрения?
При близорукости хрусталик обладает «чрезмерной» оптической силой, то есть он преломляет падающие на него лучи сильнее, чем следует. Поэтому лучи, идущие от удаленного источника света, то есть практически параллельные, при полностью расслабленной глазной мышце собираются в точку не на сетчатке, как в нормальном глазу (рис. 10.14), а перед сетчаткой. Глазная мышца тут ничем помочь не может: ведь она может только увеличивать оптическую силу глаза, а в данном случае ее как раз нужно уменьшить.
Зато когда рассматриваемый предмет находится близко от глаз, никаких проблем у близорукого человека не возникает: «сильный» хрусталик позволяет хорошо рассматривать мелкие предметы, поднося их даже ближе к глазам, чем это может сделать человек с нормальным зрением.
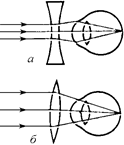 Рис. 10.15 Рис. 10.15 |
Исправить этот недостаток зрения можно с помощью очков с рассеивающими линзами, т.е. с линзами, имеющими отрицательною оптическую силу. Рассеивающая линза превращает параллельный пучок лучей от удаленного источника в расходящийся пучок, и тогда «сильный» хрусталик собирает этот пучок в точку точно на сетчатке (рис. 10.15,а).
При дальнозоркости оптическая сила хрусталика, наоборот, слишком мала, то есть он преломляет падающие на него лучи слабее, чем требуется. Из-за этого при расслабленной глазной мышце изображения удаленных предметов, от которых исходят практически параллельные лучи, получаются не на сетчатке, как у нормального глаза, а за сетчаткой (см. рис. 10.14).
Для того чтобы эти изображения получались на сетчатке, глазной мышце приходится напрягаться. Но чем ближе предмет, тем сильнее приходится преломлять исходящие от него лучи, а возможности глазной мышцы ограничены. Поэтому, начиная с определенного расстояния, даже при максимальном напряжении глазной мышцы хрусталик не может дать изображение предмета на сетчатке. Напомним, что у нормального глаза такое расстояние составляет примерно 10–12 см, а у дальнозоркого глаза оно может быть и 50 см, и 100 см, и 3 м! Поэтому-то сильно дальнозоркие люди и не могут читать книги без очков. (А близорукие – запросто!)
Дальнозоркому глазу нужно «добавить» оптическую силу, то есть помочь ему сильнее преломлять попадающие в него лучи. Поэтому очки для дальнозорких нужны с собирающими линзами, то есть с линзами, имеющими положительную оптическую силу (рис. 10.15, б). Вообще линза очков и хрусталик глаза действуют как составная линза: их оптические силы складываются, давая в сумме оптическую силу хрусталика нормального глаза.
СТОП! Решите самостоятельно: А6, В10, С6, С7.
Задача 10.6. Найти оптическую силу очков, восполняющих недостаток дальнозоркого глаза, для которого расстояние наилучшего зрения d1 = 50 см.
| d1 = 50 см | Решение. Пусть Dг – оптическая сила человеческого глаза в состоянии наилучшего зрения, а f – расстояние между хрусталиком и сетчаткой. |
| D0 = ? |
Когда глаза человека находятся в состоянии наилучшего зрения (например, при чтении книги), то можно применить формулу линзы:
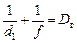
После того, как человек надел очки, расстояние наилучшего зрения стало равно d0 = 25 см, а оптическая сила «составной линзы» «глаз+очки» стала равна D0 + Dг. Тогда формула линзы будет иметь вид:
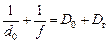
Вычтем из уравнения (2) уравнение (1), получим:
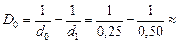
Следовательно, человеку надо носить очки с оптической силой 2,0 дптр.
Ответ: 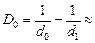
Читатель: По-моему, к такому же результату можно придти иначе. Надо, чтобы линза очков, расположенная на расстоянии d0 = 25 см от книги, давала мнимое и прямое изображение на расстоянии наилучшего зрения для дальнозоркого человека: d1 = 50 см (рис. 10.16). Тогда в формуле линзы d = d0; f = –d1, а D0 – оптическая сила очков, и формула линзы примет вид 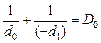
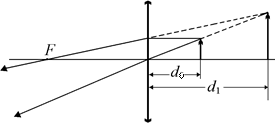
Автор: Вы совершенно правы. Запомним эту формулу:
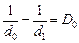
СТОП! Решите самостоятельно: А7, В11, В12.
Задача 10.7.Человек может отчетливо видеть небольшие предметы на расстоянии не дальше d1= 50 см от глаз. Какие ему нужны очки?
| d1= 50 см | Решение. Человек с нормальным зрением, а также человек, имеющий дальнозоркость, на больших расстояниях все предметы видят отчетливо. |
| D0 = ? |
Если же человек плохо различает детали предметов, удаленных дальше определенного расстояния, значит, у него близорукость. Когда близорукий человек рассматривает удаленные предметы, его глазная мышца полностью расслаблена.
Пусть Dг – оптическая сила хрусталика глаза человека при расслабленной глазной мышце, f – расстояние от оптического центра хрусталика до сетчатки (это расстояние называется еще глубиной глаза) (рис. 10.17).
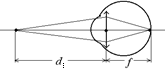 Рис. 10.17 Рис. 10.17 |
Так как по условию задачи при оптической силе хрусталика Dг изображение предмета, удаленного от глаза на расстояние d1, получается на сетчатке, то есть на расстоянии f за хрусталиком, то для хрусталика глаза, как для собирающей линзы, можем записать формулу линзы:
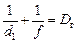
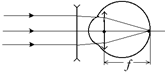 Рис. 10.18 Рис. 10.18 |
Очки должны полностью исправить недостаток зрения. Значит, после того, как к оптической силе хрусталика добавится оптическая сила линзы очков при полностью расслабленной глазной мышце изображения предметов, удаленных на большое расстояние d1 ® ¥, должны получаться точно на сетчатке (рис. 10.18).
Так как оптическая сила составной линзы «хрусталик + линза очков» равна сумме оптических сил этих линз: Dг + D0, где D0 – оптическая сила линзы очков, то можно записать формулу линзы для случая, когда человек в очках рассматривает удаленные предметы на расстоянии d2 ® ¥:

Дробь 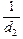
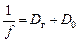
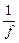
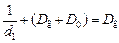
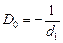
Подставим численные значения:
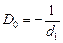
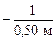
Ответ: 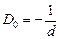
СТОП! Решите самостоятельно: А8, В14.
Задача 10.8.Мальчик читает книгу без очков, держа ее перед собой на расстоянии: d1 = 10 см. Какие очки следует носить мальчику?
| d1 = 10 см = 0,10 м | Решение. Если бы зрение у мальчика было нормальным, он держал бы книгу на расстоянии наилучшего зрения: d0 = 25 см |
| D0 = ? |
перед собой. Очки должны исправить недостаток зрения. Значит, после того, как мальчик наденет очки, он при таком же напряжении глазной мышцы будет держать книгу на расстоянии d0 = 25 см от глаз.
Пусть f – глубина глаза, Dг – оптическая сила хрусталика глаза при «настройке» на расстояние наилучшего зрения, D0 – искомая оптическая сила очков, d1 – расстояние, на котором мальчик держит книгу, читая без очков. Тогда мы можем записать формулу линзы для этих двух случаев:
1) мальчик читает книгу без очков:
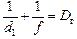
2) мальчик читает книгу в очках:
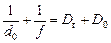
Подставим значение Dг из (1) в (2), получим:
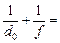
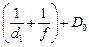
Отсюда получаем уже знакомую нам формулу:
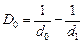
Подставим численные значения:
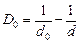
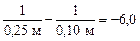
Ответ: 1) 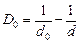
СТОП! Решите самостоятельно: А9, В13, В15, D2.
Дата добавления: 2016-04-11 ; просмотров: 3154 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Источник