Число фидия золотое сечение

Найти золотую середину, или тайны золотого сечения

Число Ф (фи), которое называют золотым сечением или серединой, является одним из самых загадочных терминов в математике и физике. Интересно, что оно часто встречается в повседневной жизни, хотя многие об этом никогда не задумывались. Даже люди, не знакомые с правилом золотого сечения, видят его, сами того не понимая. Проводились эксперименты: испытуемым показывали случайные лица и просили назвать наиболее привлекательные. Таковыми оказывались лица, в которых находили золотые соотношения между различными величинами – шириной лица, глаз, линии бровей, носа. Таким образом, инстинктивно человек видит приближенное к пропорциям, которые считаются идеальными.

Что такое золотое сечение?

Это пропорция, полученная делением в крайнем и среднем отношении. Также это называют гармоническим делением. Как вычисляется золотая середина? В выражении математическим языком эта величина представляет собой соотношение двух величин a и b, где известно, что а>b, и имеет место такое равенство: a/b=(a+b)/a. Представив, что a и b – это части одного отрезка, можно сказать: отношение меньшей части к большей равно отношению большей части к целому. Золотое сечение обозначают 21-й буквой греческого алфавита – Ф (произносится как «фи»).

Данное число бесконечно, как и Пи, показывающее отношение длины окружности к диаметру. Выглядит оно так: 1.6180339887498948420… Соответственно, округляют Ф до 1,618.

История золотого сечения

У этой величины несколько названий. Среди них – божественная пропорция и асимметричная симметрия. Считается, что в науку метод золотого деления внес Пифагор в VI веке до нашей эры. В свою очередь он узнал об этом у египтян и вавилонян. Ведь то, что они использовали соотношения золотого деления доказывают пропорции пирамид, храмов, барельефов, предметов быта и украшений.

Встречается данное правило и в другой древней архитектуре. Например, пирамида Гизы имеет высоту 146,6 метров, а каждая сторона основания достигает 230,5 метров. Если рассчитать отношение длины стороны к высоте, получаем 1,5717, а это совсем рядом со значением Ф. Греческий скульптор и математик Фидий, живший в V веке до нашей эры с применением правила золотого деления создавал скульптуры для Парфенона. Универсальным связующим звеном математических отношений назвал золотое сечение Платон. А Евклид еще в IV веке до нашей эры увидел золотое сечение в пентаграмме.

С данным понятием непосредственно связана последовательность Фибоначчи. Известный математик создал последовательный ряд чисел, и если взять любые два очередных числа, то их отношение будет очень близко к Ф. При этом по мере возрастания чисел, соотношение всё больше приближается к 1,618. К примеру, если взять 3 и 5, то соотношение равно 1,666, а если 13 и 21, то получается уже 1,625. Равное значению Ф дает отношение 144 и 233.

«Золотые» фигуры

Принцип золотого сечения используется для построения геометрических фигур. И считается, что полученные таким образом фигуры, выглядят наиболее изящными. Это подтверждают многократно проведенные эксперименты. Внимание испытуемых больше привлекают именно такие фигуры.

Самым простым примером является прямоугольник, при вычислении отношения сторон которого получаем значение Ф. Еще один замечательный пример – правильный пятиугольник. Все его диагонали делят друг друга на отрезки, связанные золотой пропорцией, а каждый конец – это золотой треугольник. При вершине такого треугольника образуется угол в 36 градусов, а основание делит боковую сторону в пропорции золотого сечения. Внутри пятиугольника строится пентаграмма.

Древнегреческий ученый Архимед, первым отметил, что если от золотого прямоугольника последовательно отсекать квадраты, соединяя противоположные точки четвертью окружности, получается изящная спираль.

Золотое сечение в изобразительном искусстве

В эпоху Возрождения при создании картин и скульптур великие мастера применяли золотое сечение, чтобы достичь баланс красоты. Наиболее яркими примерами являются творения Леонардо да Винчи. С помощью этого правила художник определял пропорции в работе «Тайная вечеря». Это видно при исследовании размеров стола, стен, элементов интерьера. Также божественная пропорция прослеживается в картинах «Мона Лиза» и «Витрувианский Человек». Такие великие художники, как Микеланджело, Рафаэль, Рембрандт, Сальвадор Дали и другие, использовали золотое сечение при создании своих шедевров.

Примеры золотого сечения в жизни и в природе

Ежедневно мы можем наблюдать идеальные пропорции:

• Грудная и брюшная части тела бабочки соотносятся в золотой пропорции. А при сложенных крыльях это прекрасное создание представляет собой правильный треугольник с равными сторонами.
• У стрекозы длины хвоста и корпуса относятся так же, как общая длина тела к хвосту.
• В пропорциях тела ящерицы также прослеживается данный принцип.
• Большинство яиц птиц можно вписать в золотой прямоугольник.
• Последовательность Фибоначчи видна в развитии растений, в расположении чешуек в шишках, зерен в подсолнухах.
• Спирально растет бараний рог, плетет паутину паук.
• Интересно, что если напугать стадо северных оленей, то животные будут разбегаться по спирали.
• В форме двойной спирали представлена молекула ДНК.
• Цветки разных растений, а также морские звезды имеют форму правильного пятиугольника.

Как видно, примеров с правильными пропорциями в природе и повседневной жизни предостаточно. Не даром золотое сечение называют божественной пропорцией. Вероятно, именно этим правилом руководствовался создатель в процессе заполнения Вселенной живыми и неживыми объектами. То, что соответствует этому правилу, кажется нам наиболее привлекательным.

В мире много интересных вещей, изучение нового делает нас умнее, способствует развитию мозга и мышления. Советуем вам обязательно находить время на познание нового. А чтобы было легче усваивать и запоминать большие объемы информации, рекомендуем тренажеры Викиум. Регулярно используя их для тренировок мозга, вы сможете улучшить память, внимательность, логику и аналитические способности.

Источник

Что такое «золотое сечение»?

На протяжении веков «золотое сечение» считается самым прекрасным соотношением в искусстве и архитектуре.

«Золотое сечение», называемое также «золотая пропорция» или «золотое соотношение», было обнаружено во многих самых знаменитых творениях человечества — от древнегреческого Парфенона до творений Сальвадора Дали. Возможно, вы уже читали на эту тему статью «Нереализованное влияние золотого сечения».

Не важно, считаете ли вы, что эта божественная пропорция является поистине знамением красоты или просто предвзятым выбором, но, без сомнения, это одно из самых интригующих чисел в мире. Поэтому, сейчас мы поговорим о математической основе «золотого сечения».

Впервые о «золотом сечении» упоминает древнегреческий математик Евклид около 300 лет до нашей эры. В шестой книге своего трактата «Начала» Евклид дает определение «золотого сечения». Он поручает нам взять отрезок линии и разделить его на два меньших сегмента так, что отношение всей линии (a + b) к отрезку a будет таким же, как отношение отрезка a к сегменту b:

Что эквивалентно пропорции:

Евклид использовал «золотое сечение» для построения правильного пятиугольника. Отношение диагонали правильного пятиугольника к его стороне равно золотому сечению. Правильный пятиугольник (пентагон) еще называют «золотой пятиугольник».

Золотой прямоугольник

«Золотое сечение» часто представляют как «Золотой прямоугольник» — прямоугольник с отношением длин сторон примерно 1,618:1.

Этот прямоугольник обладает тем свойством, что если от него отрезать квадрат, то снова получится золотой прямоугольник меньшего размера и так до бесконечности.

На самом деле, соотношение сторон «золотого прямоугольника» — это иррациональное значение 1,618034…, т.е. бесконечная десятичная дробь, не имеющая периода.

Это число и есть пропорция «золотого сечения», оно обозначается греческой буквой Фи в честь древнегреческого скульптора и архитектора Фидия, мастера, воплотившего его в своих работах.

Решение «золотой пропорции»

Чтобы найти значение 1,618034…, мы должны решить пропорцию, показанную выше. Для простоты предположим, что b = 1 и a = x и найдем решение для x.

Шаг 1. Сделаем перекрестное умножение:

Источник

Откуда в подсолнухе золотое сечение?

Пропорция золотого сечения известна людям уже несколько тысяч лет и всё это время не теряет популярности как в чисто математической среде, так и среди художников, скульпторов, философов, биологов. Золотое сечение можно найти в:

Принципах перспективы и композиции фотографий

Пропорциях человеческого тела

И во множестве других, подчас весьма необычных, сфер.

Сегодня мы будем говорить о растениях.

Из труда А. Цезинга «Эстетические исследования».

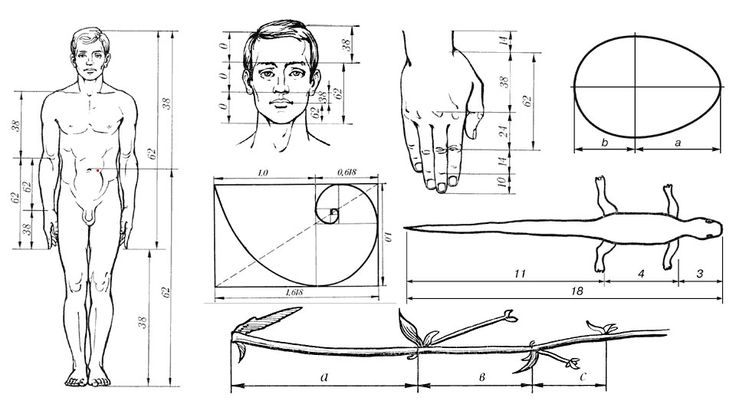
Идея золотого сечения очень проста. Возьмем отрезок, и разделим его на две части Существует единственный способ разделить отрезок на две части с длинами , так что отношение длины всего отрезка к большей части равно отношению большей части к меньшей. В самом деле, пусть длина отрезка ; по условию

Определив и немного преобразовав систему, получим квадратное уравнение:

У этого уравнения единственный положительный корень

Число называется числом Фидия или, попросту, пропорцией золотого сечения.

На заглавной картинке изображен цветок подсолнечника маслянистого — растения, масло из семян которого вы почти наверняка регулярно употребляете в пищу. С точки зрения ботаники, большой красивый цветок подсолнуха называется «соцветием-корзинкой». Желтые лепестки соцветия — видоизмененные листья; они окаймляют корзинку из крошечных желтых цветков, каждому из которых после опыления суждено превратиться в семечко. Рассматривая корзинку подсолнуха, мы можем обнаружить удивительный факт:

Человеческий глаз легко различает, как семена группируются по спиралям — левым и правым. Их число различно. Приложив усилия, можно сосчитать, что в цветке подсолнуха на фотографии 21 спираль идет по часовой стрелке и 34 спирали — против часовой. Количества подобных спиралей называются в ботанике парастическими числами (parastichy numbers). Интересно то, что что близко к . Это не случайно.

Ещё больше примеров парастических чисел

Оказывается, у множества видов растений у здорового, неповрежденного цветка или розетки имеется тенденция к выбору в качестве парастических чисел двух соседних чисел следующего ряда:

Эта последовательность широко известна как последовательность Фибоначчи. Она начинается с двух единиц; каждое следующее число последовательности — сумма двух предшествующих. У ряда Фибоначчи много замечательных свойств, главным из которых для нас является то, что отношение двух соседних членов стремится к . Этот замечательный факт напрямую вытекает из явной формулы для чисел ряда Фибоначчи, так называемой формулы Бине:

Как можно видеть, отношение двух соседних членов ряда Фибоначчи быстро стремится в . На самом деле, это характерно для любого рекуррентного ряда, строящегося по формуле «каждый следующий член равен сумме двух предыдущих».

Откуда же члены последовательности Фибоначчи взялись в цветке?

Процесс формирования корзинки называется филлотаксисом. Внутри центральной части корзинки подсолнуха — меристемы — происходит деление зародышевых клеток, образующих сначала цветок, а потом и семечко. Сразу после рождения цветок начинает выталкиваться младшими братьями и сестрами в радиальном направлении от центра.

Закон движения единичного цветка в корзинке проще всего описать в радиальной системе координат — по радиусу и углу. Для цветка номер из рожденных меристемой, его радиальные координаты описываются примерно так:

Помимо и мы видим здесь два параметра — и . — некая постоянная величина, связанная с размерами цветка в соцветии.

Закон радиального выталкивания легко обосновать физически, приняв за внимание, что цветки соцветия приблизительно одинакового размера и должны покрывать собой всю свободную площадь корзинки. Интереснее закон направления . Он зависит от константы , которая для подсолнуха с высокой точностью равна

Иными словами, порождая цветок, меристема задает ему направление движения, каждый раз меняя его это направление относительно предшествующего поворотом на .

Примерно таким образом

Это число, , неявным образом закодировано в геноме растения. Для того, что бы понять, что это и откуда оно берется, разделим его на , то есть вычислим, какую долю полного оборота оно составляет:

Вот где прячется золотое сечение! Но зачем оно нужно растению?

Для ответа на этот вопрос, обратимся к уникальному свойству числа— его разложению в цепную дробь.

Любое действительное число можно представить следующим способом:

Где целое число; прочие натуральные числа. Такое представление называется цепной дробью. Если число — рациональное, его представление в виде цепной дроби насчитывает конечное число членов, и вычисляется посредством алгоритма Евклида. В противном случае, представление числа в виде цепной дроби выражается бесконечной последовательностью знаменателей. Например, знаменитое число расписывается в виде цепной дроби вот так:

Наиболее важным свойством цепных дробей для математики является то, что они кодируют наилучшие рациональные приближения данного числа. В самом деле, попробуем «обрезать» дробь по одной из контурных линий. Мы получим рациональное число, приблизительно равное . Утверждается, что для каждого из них не существует рационального числа с меньшим знаменателем, более близкого к :

Вычисления взяты из замечательной книжки В. Арнольда «Цепные дроби»

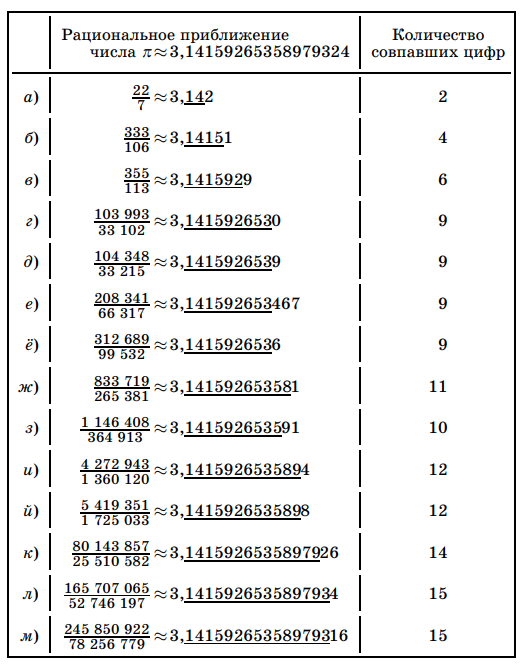
Сравните приближение и

И в том и в другом случае мы получили 6 значимых цифр после запятой, но в одном случае знаменатель — 113, а в другом — 10000000. Разница, как говорится, налицо.

Теперь, наконец, разложим в цепную дробь. Получится следующее:

Рациональные приближения, полученные посредством обрезания этого представления, выглядят так:

Легко видеть, что это ни что иное, как отношения соседних членов ряда Фибоначчи. И вот теперь, сравнивая цепочку рациональных приближений числа с аналогичной цепочкой числа мы можем видеть главное математическое свойство пропорции золотого сечения.

Для любого достаточно большого , у больше рациональных приближений со знаменателем меньше чем , чем у любого другого иррационального числа.

В самом деле. Приближая , мы видим, что уже у седьмого приближения знаменатель вырос до 99532. Узнаменатель седьмой дроби — 34. Алгоритм вычисления рационального приближения из частичного представления цепной дроби прост, и мы не будем его здесь приводить. Выведя его, легко видеть, что чем меньше числа в ряду, тем меньше будут представления, а натуральных чисел меньше, чем ряд из последовательных единиц, нельзя и представить. Одновременно с этим, является наиболее плохо приближенным числом из всех, в том смысле, что с ростом знаменателя число угаданных знаков приближения растет максимально медленно, насколько это возможно. Этот факт является прямым следствием из теоремы Гурвинца и его доказательство довольно занудно, так что мы не будем включать его в данную статью.

Суха теория, друзья, но древо жизни пышно зеленеет. Настало время сложить всё вышесказанное, и понять, как связаны: филлотаксис подсолнуха, угол , последовательность Фибоначчи, цепные дроби и рациональные приближения. И вместо того, что бы рассказать, лучше показать:

Перейдя по ссылке, вы увидите небольшую онлайн-демонстрацию процесса формирования корзинки подсолнуха. Вы можете регулировать угол порождения меристемой цветков и их количество, или изучать спирали, полученные путем выделения каждого ного зерна, начиная с первого, где n (ранг) — знаменатель одно из рациональных приближений для выставленного вами угла. Вы увидите, что при углах и некоторых других зерна в корзинке распределены почти равномерно, а число рациональных приближений с небольшим основанием максимально; для других углов число рациональных приближений невелико, а зерна подсолнуха четко группируются в спирали, причем их число соответствует знаменателю дроби того или иного рационального приближения выставленного угла. И глядя на это, даже не оперируя сложной математикой вы можете дать правильный ответ на поставленный в заголовке вопрос:

Золотое сечение в подсолнухе обеспечивает наиболее равномерное распределение семян в корзинке за счет наихудшего его приближения рациональными числами и максимизации числа спиралей небольшого ранга, вдоль которых упорядочены семена.

Настоящая статья написана по мотивам кружковых занятий Малого Мехмата МГУ для старших классов. В статье использованы следующие источники:

А. Цезинг «Эстетические исследования»

А. Щетников «Загадки филлотаксиса» (видео)

«Special Topics — Lessons from Biology for Engineering Tiny Devices / Lessons 12: Spirals and phyllotaxis» — цикл популярных лекций Принстонского университета, посвященных спиралям.

Takuya Okabe, Atsushi Ishida and Jin Yoshimura — The unified rule of phyllotaxis explaining both spiral and non-spiral arrangements — более строгое математическое описание процесса развития цветка.

Источник